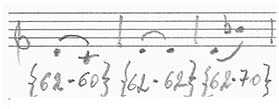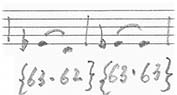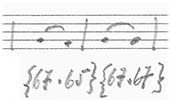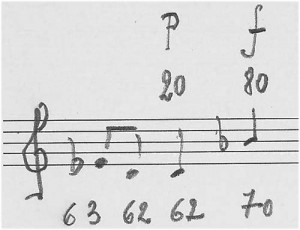1 -Introduction
Pourquoi composer avec des systèmes probabilistes ? L’indéterminisme peut-il apporter des solutions intéressantes à la musique ? Ces questions me sont venues à l’esprit lorsque je commençais la composition de Pluton, en 1988 à l’IRCAM, avec l’aide du mathématicien américain Miller Puckette. Ma principale préoccupation de l’époque était de faire sortir la musique électronique en temps réel du rôle passif qui jusqu’alors était le sien. La plupart des œuvres en temps réel (y compris dans certains moments de mes propres compositions, comme Jupiter composé juste avant) utilisaient la musique électronique surtout comme un prolongement de l’instrument. Celle-là produisait des transformations du son instrumental, parfois synchrones et parfois avec des retards mais, encouragés en cela par les tout nouveaux systèmes de suivi de partitions, quelques compositeurs donnaient la primauté à l’instrumental qui assurait la domination temporelle de toute la musique électronique. L’instrument était devenu le maître du temps, s’opposant en cela à des décennies de musique mixte au cours desquelles les instrumentistes devaient se caler sur une bande magnétique d’une rigidité temporelle très contraignante. Cette domination du temps instrumental était un atout majeur pour le développement de toute la musique en temps réel mais comprenait un écueil : l’instrument précédait l’électronique mais jamais le contraire ne se produisait, d’où parfois le sentiment que l’électronique n’était qu’un coloriage, un habillage, ne produisant que rarement un discours autonome. En exagérant quelque peu, je me disais qu’il fallait trouver un moyen pour que la musique électronique en temps réel sorte de son rôle d’accompagnement, et puisse produire, comme un véritable orchestre, un discours musical qui s’articule, se déploie indépendamment de tout déclenchement instrumental. Je réécoutais Mantra de Stockhausen – l’œuvre proprement initiatique pour moi de toute la musique en temps réel – et comparais les textures de cette musique électronique avec des œuvres plus anciennes du même compositeur, et en tout premier lieu, Kontakte. Il était clair que, malgré la présence de la bande magnétique dans cette dernière, empêchant toute modulation temporelle, la musique électronique y était beaucoup plus travaillée, autonome et plus riche que dans Mantra. Ce qu’il fallait faire, me disais-je à cette époque, c’était conserver les acquis du temps réel tout en permettant à la musique électronique de prendre son essor dans des textures polyphoniques aussi travaillées que ce fut le cas dans les anciennes musiques composées pour bande magnétique. La situation principale du temps réel était marquée par le sceau de l’incertitude temporelle. Comme pour la musique instrumentale, il est souvent impossible de savoir avec exactitude quand va intervenir le prochain événement. Nous pouvons en avoir une « connaissance floue » mais rarement exacte. Lorsqu’un interprète fait un point d’orgue, prend un tempo particulier, fait un ralenti ou un accéléré, il est impossible de connaître la durée exacte d’une phrase. Il fallait alors concevoir des méthodes de composition qui puissent être « infinies » dans le sens où la musique électronique durerait le temps qu’elle doit durer, compte tenu de cette absence de connaissance temporelle dans le futur. La machine devra travailler et produire des séquences musicales pendant un temps variable qui sera toujours différent d’une exécution à l’autre. C’est alors que l’idée d’utiliser des systèmes indéterministes s’est présentée clairement à mon esprit. Si la durée du temps devant nous est inconnue, alors les structures qui vont l’habiter devront participer de cette incertitude. Désormais, on ne va pas conclure, faire une transition, une progression, bref, une grande partie des stratégies compositionnelles que l’on connaît déjà. Non, on va créer des états sonores qui doivent exister en tant qu’états, mais se renouvelant sans cesse. Ou bien des états qui vont se transformer en d’autres états. La machine devra calculer sans cesse et produire en temps réel une musique qui naîtra au moment même où on l’entend. Les ordinateurs, de façon très générale, ne savent faire que trois choses :
- Ils font ce qu’on leur ordonne de faire. C’est un processus déterministe dans lequel on pose un problème que la machine va traiter, calculer, jusqu’à sa résolution. Dans la musique, le cas typique de ce mode d’action est la composition algorithmique dans laquelle tous les paramètres sont indiqués dans le programme qui tourne ainsi en « interne » suivant les procédures qu’on lui a données. J’ai une suite d’intervalles et je donne des règles pour les regrouper en accords. La machine va explorer la totalité des possibilités, puis arrêter son calcul lorsque celle-ci sera atteinte.
- Ils prennent des informations dans le monde extérieur. Via un micro, une caméra, un capteur quelconque, un ordinateur peut se saisir d’informations extérieures, les analyser, puis les traiter. En musique cela concerne tous les systèmes de traitement, de suivi de partitions, de détection d’événements sonores en temps réel. Les paramètres, contrairement à la méthode précédente, ne sont pas connus à l’avance même si, comme c’est le cas du suivi de partitions, ils peuvent être « reconnus » parmi un flot sonore. La machine se nourrit alors de données externes pour faire marcher son programme et ne produit rien tant que ces informations ne lui sont pas données.
- Ils produisent des nombres aléatoires. Il s’agit de la seule manière que l’on connaisse pour « donner la main » à un processeur de calcul afin qu’il agisse de façon autonome. Ils peuvent produire de l’aléatoire le temps que l’on veut sans autre forme de calcul ou de captation. Le processeur tourne de nouveau en « interne » (comme dans a) mais sans apport aucun de paramètres extérieurs[1].
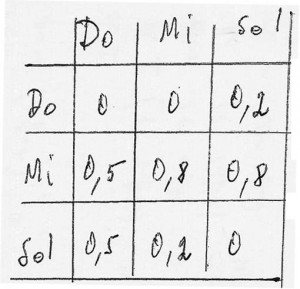
C’est donc cette dernière solution qui m’a d’abord semblé la plus adéquate à la situation que j’ai décrite plus haut. Mais très vite je me suis rendu compte que ce serait la conjonction des deux dernières méthodes qui serait la plus intéressante : la machine produira de l’aléatoire, mais à partir d’éléments fournis par les interprètes. J’avais trouvé la façon de produire une musique électronique autonome et non simplement réactive au monde instrumental et, à la fois, de laisser ce travail s’exécuter pendant un temps qu’a priori je ne pouvais pas définir. Le procédé des chaînes de Markov est venu très rapidement à mon esprit comme la meilleure façon de traiter ce problème car il se charge d’une situation bien connue des musiciens, celle de la succession des événements dans le temps. Qu’est-ce qui fait que la succession de certains intervalles dans un contexte donné produise un sens musical tandis qu’une autre succession n’en produit aucun ? Comment se fait-il que, en écoutant certaines musiques, nous sommes parfois capables de deviner ce qui va suivre ? De nombreuses réponses à ce problème sont bien connues, ce ne sera donc pas le thème de ce papier. Mais il faut admettre que l’ordre de succession des événements musicaux est d’une importance aussi grande que les événements eux-mêmes. C’est lui qui donne un « sens » à ce que nous écoutons. Une question m’avait préoccupé lors de mes études musicales : à quoi reconnaît-on une mélodie comme typique de telle ou telle œuvre ? J’avais même passé mon prix d’analyse musicale au Conservatoire de Paris en faisant un relevé statistique de toutes les mélodies qui se trouvent dans une section de la Grande Fugue de Beethoven. À la suite de fastidieux calculs, j’avais déterminé des pourcentages pour qu’après un intervalle a apparaisse un intervalle b, c ou d. J’avais ensuite reconstitué des chaînes mélodiques qui ne se trouvaient aucunement dans l’œuvre de Beethoven mais qui, obéissant à ces statistiques de successions, avaient des airs de familiarité avec les mélodies que l’on trouve dans la Grande Fugue. La raison pour laquelle le premier prix d’analyse m’avait été accordé à la présentation de ce travail est restée pour moi, jusqu’aujourd’hui, un grand mystère ! Il est évident que les mélodies, très curieuses et excentriques composées par Beethoven, même dans une œuvre aussi radicale et révolutionnaire que sa Grande Fugue, reposent toujours sur un substrat harmonique et ne sauraient être expliquées d’un simple point de vue statistique de successions d’intervalles. Mais, comme cela arrive parfois, un point de vue totalement subjectif – voire erroné – sur une œuvre apporte parfois plus d’idées créatrices qu’une étude, plus juste et rationnelle, mais dépourvue de toute vision subjective[2]. Mon angle d’analyse n’expliquait pas grand chose quant à cette œuvre de Beethoven, mais j’avais néanmoins appris une propriété intéressante de la musique : elle a beau se dérouler dans le temps, il existe néanmoins des structures dont le sens musical ne repose pas sur un quelconque ordre temporel. Quel que soit l’ordre (et en ce sens le calcul probabiliste permet de le renouveler en permanence) dans lequel les éléments de cette structure seront distribués, cette dernière sera identifiée comme telle. Ainsi si je dis « accord de do majeur », je peux accepter les ensembles {do, mi, sol}, {do, sol, mi}, {mi, do, sol}, {mi, sol, do}, etc., chacun attestant parfaitement la propriété de « accord de do majeur ». L’ordre temporel n’a ici aucune importance car, dans tous les cas, la structure sera conservée et reconnue. C’est ce que Iannis Xenakis appelait les « structures hors-temps »[3]. Une des manières de réaliser ce petit exemple consiste à créer des chemins possibles entre ces notes et à définir des probabilités de successions entre elles. Ainsi les probabilités de successions {do->mi} et {do->sol} pourront être également déterminées à 0,5 (soit 50%), la somme des probabilités devant être toujours égale à 1. Cela élimine la possibilité que la répétition du do n’intervienne. Reste maintenant à déterminer les probabilités de successions à partir du mi et du sol comme par exemple : {mi->mi = 0,8 / mi->do = 0 / mi->sol = 0,2} puis {sol->sol = 0 / sol->do = 0,2 / sol->mi = 0,8}. Cet ensemble de relations peut s’écrire sous la forme d’une matrice, ce qui donne :
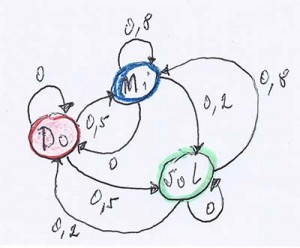
ou encore sous la forme d’un graphe :
À partir de ces probabilités, il est possible de créer une chaîne d’événements dont voici un exemple :
do mi mi mi do sol mi mi mi do sol do mi mi mi sol mi do sol do sol mi mi mi….
C’est la base de ce processus que l’on appelle les « chaines de Markov »[4].
2 – Un exemple de transition entre désordre et ordre.
Vers le milieu des années 70, j’ai utilisé un tel procédé pour contrôler des successions d’intervalles suivant une procédure dont le but était de partir d’une distribution totalement aléatoire pour arriver à un ordre totalement déterministe. Cela se produisait en plusieurs étapes, dont voici la description.
a) On tire au hasard n intervalles parmi 6 intervalles possibles : 1, pour le demi-ton, 2 pour le ton, 3 pour la tierce mineure, 4 pour la tierce majeure, 5 pour la quarte et 6 pour la quarte augmentée). Les intervalles supérieurs à 6 ne sont que des redoublements des précédents.
b) On fait une analyse statistique de cette série de n intervalles en relevant les successions obtenues à partir de laquelle on construit une matrice de probabilités.
c) On tire une nouvelle succession de n intervalles à partir de la matrice précédente.
d) On répète les étapes b et c jusqu’à ce que l’on obtienne une boucle. Certains intervalles, les moins fréquents lors de a, auront tendance à disparaître, pendant que d’autres, parmi les plus nombreux au début, tendront vers une augmentation de leur probabilités. Une fois la boucle obtenue, on arrête le processus.
Voici un exemple simplifié de ce processus.
6 1 4 5 5 6 5 1 5 4 3 5 4 5 4 3 4 6 2 3
(tirage aléatoires de 20 intervalles)
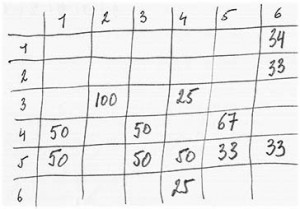
Voici la matrice résultante de l’analyse des successions précédentes :
Deuxième tirage aléatoire de 20 intervalles à partir des probabilités précédentes :
5 4 5 5 4 5 4 5 4 6 5 5 4 6 2 3 5 6 2 3
Ici, une nouvelle matrice d’analyse des successions obtenues précédemment :
Troisième tirage aléatoire de 20 intervalles à partir des probabilités précédentes :
3 5 4 5 4 5 4 5 4 6 2 3 5 6 2 3 5 4 5 4
Encore une nouvelle matrice d’analyse des successions obtenues précédemment :
Quatrième tirage aléatoire de 20 intervalles à partir des probabilités précédentes (identique au précédent):
3 5 4 5 4 5 4 5 4 6 2 3 5 4 5 4 5 4 5 4
Voici maintenant la transcription musicale avec les 4 séquences obtenues :
Mais, comme je l’écrivais au début de cet article, c’est dans le cadre de la musique électronique en temps réel que ce procédé des matrices de Markov a été le plus important. C’est dans Pluton (1988-89) que je l’ai utilisé pour la première fois.
3 – Comment engendrer des séquences aléatoires mais identifiables ?
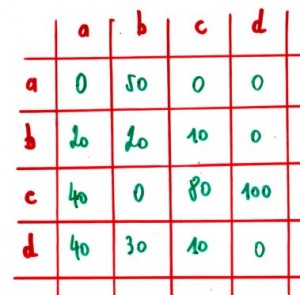
Reprenons l’exemple le plus simple d’une matrice décrivant les probabilités de succession entre 4 événements : a, b, c et d :
Nous pouvons en déduire une succession telle que : a c c c b a c c d c c c c b a b d c c c…
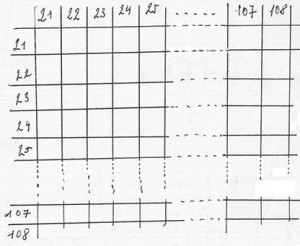
Maintenant supposons qu’au lieu d’une matrice à 4 éléments, nous en ayons une qui traite de 88 éléments ordonnés de 21 à 108 :
Cette échelle de 21 à 108 correspond, bien évidemment, aux 88 touches du clavier d’un piano dans la notation MIDI. Il s’agira donc, lorsque le pianiste jouera, de marquer les successions de note à note. Ainsi pour une séquence telle que :
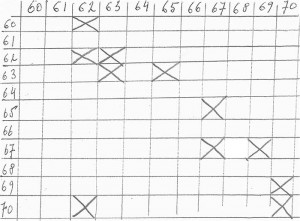
nous obtiendrons les connections suivantes (les croix indiquent uniquement qu’il existe des successions entre les notes) :
Cependant, comme il est facile de le constater, il existe plusieurs chemins en partant d’une note : 62 peut aller sur 60, 62 et 70 :
63 peut aller sur 62 ou se répéter :
67 peut aller sur lui-même ou sur 65:
Et 70 peut aller sur 69 ou sur lui-même :
Seuls 65 et 69 (le fa et le la) iront, dans tous les cas, respectivement sur 63 (mib) et 67 (sol) et leurs probabilités seront alors de 100%. Il s’agit maintenant de décider quel chemin suivre, lorsqu’il s’en trouve plusieurs qui se proposent à partir d’une même note, et d’en déduire des pourcentages. Avant de répondre à cette question, je donnerai une information complémentaire. Comme pour l’expérience de jeunesse que j’avais tentée en construisant artificiellement des mélodies dans le style de celles de la Grande Fugue de Beethoven, il s’agira ici de créer des musiques qui, même en se renouvelant constamment, ne feront que reproduire des connexions existantes. En d’autres termes, rien qui n’aura pas été joué au moins une fois, ne pourra se reproduire. Le système markovien ne crée rien qui n’ait déjà existé. Pour que ces mélodies ressemblent à celles qui ont servi de modèles, il ne suffit pas de prendre en considération les seules hauteurs, mais aussi le temps qui a été joué entre deux notes, ainsi que la valeur d’intensité. De la sorte, lorsqu’à partir de la première note de cette mélodie (mib) nous observons deux chemins possibles, nous conserverons les durées qui ont servi à effectuer ces transitions. Ainsi la transition {mib-ré} se reproduira toujours avec les valeurs de croches qui ont été jouées :
tandis que la répétition de ce même mib vers la fin se fera avec une distance de noire :
Notons que si nous reproduisons ici les valeurs sur la partition notée, dans la réalité, ce seront les valeurs interprétées (ajustées à la milliseconde près) qui seront prises en compte. Mais que se passe-t-il lorsque, comme c’est le cas ici, une même connexion se reproduit deux fois ?
Comme il ne peut y avoir qu’un seul chemin possible à partir d’une transition entre deux notes, la solution choisie est que la répétition d’une même transition effacera la première et la remplacera par la seconde. Ainsi si la transition {63-62} est répétée, la valeur de temps de la seconde occurrence (ainsi que leurs valeurs dynamiques) se substituera à la première.
Venons-en maintenant à l’établissement des probabilités de successions lorsque plusieurs chemins se proposent. La solution que j’ai choisie, mais bien arbitrairement il faut l’avouer, est que les probabilités suivront les rapports entre les valeurs dynamiques. En d’autres termes, plus une note sera jouée forte, plus sa probabilité d’apparition sera élevée, et vice versa. Ainsi pour les successions telles qu’elles apparaissent au début, nous aurons les pourcentages égaux à 100 puisqu’il n’existe, pour le moment qu’un seul chemin possible : le mib va sur le ré qui, lui se répète.
Mais, juste après il se produit une nouvelle bifurcation : le ré peut, soit se répéter, soit monter au sib. Admettons, pour la démonstration, que le ré soit joué « p » alors que le sib le soit « f » (soit par exemple avec les valeurs de 20 et 80 sur une échelle d’intensité de 100), les pourcentages se déduiront alors ainsi :
Ainsi, lors du jeu du pianiste, le processeur produit une sorte de double en temps réel en créant un discours probabiliste qui ne contient cependant que ce qui a été strictement joué. Résumons la situation. Comment cela se passe-t-il dans la continuité ?
1) Le piano joue une séquence qui, via le protocole MIDI, est envoyé à la matrice de Markov. Chaque transition mémorise les hauteurs concernées, leurs niveaux dynamiques ainsi que le temps entre chaque transition.
2) Dès le début, lorsqu’elle reçoit les premières informations venant du piano, la matrice de Markov est active. A chaque nouvelle note produite s’effectue un tirage aléatoire (un nombre entre 0 et 99) qui déterminera quelle note vient ensuite.
4 – Incrustations des structures musicales.
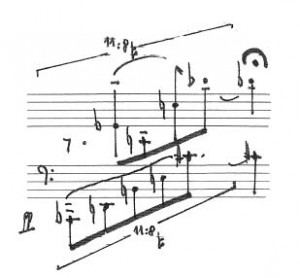
Voici un exemple, extrait de mon œuvre Pluton pour piano et électronique en temps réel (1988-89), dans lequel différentes structures musicales sont incrustées les unes dans les autres. La première précaution à prendre est évidemment de faire le maximum pour que ces structures ne se confondent pas. Voici donc une première séquence dont les caractéristiques principales sont de se dérouler dans l’extrême aigu du clavier et dans un tempo très vif :
(Piano solo : Ilmo Ranta)
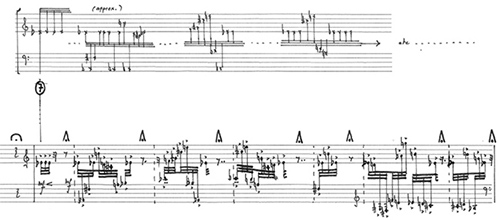
Le fait que cette séquence contient plusieurs retours sur les mêmes notes, mais qui sont suivies de notes différentes assure un renouvellement constant de la séquence produite par les chaînes de Markov. Chaque note, revenant 5 ou 6 fois, est à chaque fois suivie d’une note différente, le nombre de chemins possibles se multiplie donc assez rapidement. Une deuxième structure intervient maintenant qui se démarque de la précédente par son ambitus, situé plutôt dans le médium, et son tempo, moins constant et plus modéré que celui de la première séquence :
Si ces deux structures diffèrent grandement quant à leur ambigus et leurs tempi, elles comportent cependant plusieurs notes en commun. Les notes entourées en noir et en rouge (le do aigu et le ré) appartiennent aux deux séquences et lors du tirage aléatoire, le système markovien choisit alors de continuer soit dans la première séquence, soit de passer à la seconde. Les temps de stagnations ou de passages entre ces séquences étant dépendants du choix aléatoire, il s’opère un constant renouvellement structurel par l’absence totale de régularité. On entend alors clairement que la première séquence (aiguë et rapide) est peu à peu contaminée par la seconde (medium et modérée) :
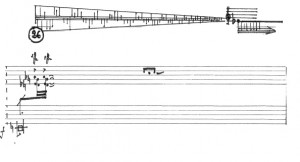
Vient ensuite un troisième niveau avec une autre séquence, celle-ci déroulée dans le grave et dans des durées beaucoup plus longues. Cette troisième séquence comporte son propre matériel, mais aussi des notes en commun avec la deuxième (entourées en bleu et en vert) et aussi avec la première (entourée en rouge). Trois niveaux s’interpénètrent donc, du plus aigu au plus grave et du plus vif au plus lent, et se contaminent les uns les autres :
Il est clair que plus le nombre de chemins devient grand, plus les caractéristiques dominantes du début tendent à disparaître. Ainsi, avec le temps, on ne remarque la présence de la première séquence (notes très rapides et aiguës) que sporadiquement, l’ensemble de ces processus donnant naissance à une forme en perpétuel changement. On peut ainsi « incruster » un grand nombre de séquences les unes dans les autres, le système produira toujours des transitions entre elles, cela pour l’histoire immédiate, mais dans la grande histoire (si je puis m’exprimer ainsi au niveau d’une œuvre) se produiront des changements structurels constants par le fait que de nouvelles structures viendront peu à peu effacer le souvenir des anciennes. Il se crée donc une forme en perpétuelle évolution qui, au fur et à mesure qu’elle accueille de nouvelles structures, a tendance à éliminer les plus anciennes.
5 – Comment le son est-il produit ?
Comment ce résultat aléatoire se transforme-t-il en matière sonore ? Ce que produisent les matrices de Markov n’est ni plus ni moins qu’une partition virtuelle qui se crée en temps réel et se régénère d’elle même. Dans Pluton la partition calculée à partir des chemins markoviens va agir directement sur un échantillonneur. Ce module mémorise un son de piano (qui peut être une simple note comme un accord ou une figure quelconque) qui va être transposé suivant les hauteurs fournies par la matrice. Par convention, la hauteur 63 (le mib du milieu du clavier de piano) correspond à la fréquence originale de l’échantillon. Ainsi l’accord échantillonné suivant :
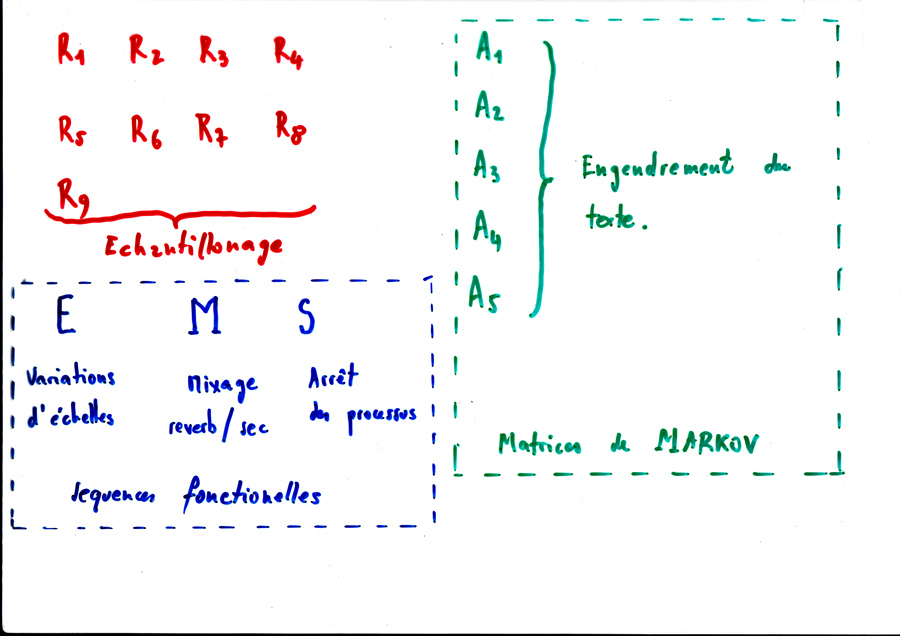
sera joué tel quel lorsque la matrice produira la hauteur 63. Lorsqu’elle produira 64, cet accord sera transposé au demi-ton supérieur et pour 62, au demi-ton inférieur, etc. La partition, vue par pianiste, est organisée ainsi :
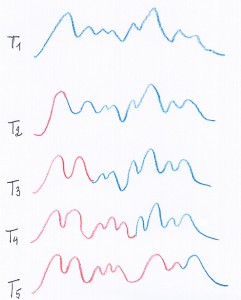
Sur la partie droite (en vert) se trouvent 5 séquences destinées à nourrir les matrices de Markov, telles que j’en ai exposé certaines précédemment. Sur la partie gauche (en rouge) se trouvent des séquences d’échantillonnage. Les deux processus s’interpénètrent ad libitum dans ce qu’il est convenu d’appeler une « forme ouverte », c’est-à-dire une forme dans laquelle l’ordre de succession des séquences est laissé à l’appréciation de l’interprète. Contrairement aux célèbres formes ouvertes, telles que la Troisième sonate pour piano de Boulez, le Klavierstück XI de Stockhausen ou encore les Archipels de Boucourechliev, œuvres où l’ « ouverture » de la forme n’est pas audible mais n’existe que conceptuellement pour l’interprète, la forme ouverte ici aura une répercussion immédiate sur la musique électronique et s’entendra comme telle. Le déroulement de cette musique ne sera pas le même suivant les chemins parcourus par le pianiste. Pour faire une comparaison, je dirais que les séquences markoviennes constituent la partition en terme de hauteurs, de dynamiques et de temps, tandis que les séquences d’échantillonnage représenteraient plus un travail d’orchestration. En termes plus précis, les séquences échantillonnées dans la partie gauche (en rouge) seront transposées sur les hauteurs, avec les durées et les intensités produites par le résultat des calculs aléatoires sur les matrices de la partie droite. Il est possible de modifier à tout moment cette orchestration, c’est-à-dire de changer l’échantillon qui sera transposé par les matrices. Cela se fait grâce à un système, inventé par Miller Puckette, qui était très nouveau à l’époque où je l’ai utilisé. Il s’agit d’un procédé d’échantillonnage à la volée. L’échantillonneur lit une table d’onde correspondant au son échantillonné en cours. Lors d’un nouvel échantillonnage, il substitue progressivement l’ancien échantillon par un nouveau. Le graphique suivant donne un aperçu de ce procédé : l’onde dessinée en bleu est la première qui est progressivement remplacée aux temps T1, T2, T3, etc. par une nouvelle (marquée en rouge). Cela se produit en temps réel au moment même de l’enregistrement et sans arrêt du son ni, fort heureusement, sans les « clics » habituels que l’on entend dans ce genre d’opération :
Voici quelques exemples de ce procédé. Ici une série d’accords, lorsqu’ils vont être joués, vont servir d’échantillons pour la production des séquences markoviennes. On entend très bien les changements harmoniques ainsi que les variations d’intensités qui sont répercutées en temps réel sur la partition qui ne cesse pas de se régénérer :
Un autre exemple est donné ici par la séparation en deux voix des processus markoviens. Deux matrices tournent en parallèle avec le même contenu. Il est évident que même dotées de probabilités identiques, les matrices parallèles produisant des tirages aléatoires ne reproduiront jamais le même résultat. L’une des matrices se servira du premier échantillon joué, un trille, tandis que l’autre se servira du second, un accord. Chacune d’entre elle est alors « orchestrée » de manière différente :
Le même procédé est utilisé ici, mais avec un arpège et un accord staccato. Il faut bien comprendre que la partition jouée par cet arpège en reproduira une transposition différente pour chaque note produite par la matrice de Markov :
Là se fait jour une loi de perception propre à ce genre de musique. Cette loi, qui nulle part n’est exprimée, repose sur la relation entre un son de référence et son organisation musicale. Par son de référence j’entends l’élément qui va être échantillonné et transposé sur les hauteurs fournies par les chaînes de Markov. À ce stade le son de référence devient un « instrument ». Si ce son est simple, voire consistant en une seule note, la partition qu’il donnera à entendre révèlera sa propre structure, car les hauteurs comme les durées seront clairement exprimées. Une partition indiquant « do, mi, sol » sonnera comme « do, mi, sol ». Mais lorsque le son de référence devient plus complexe, c’est-à-dire qu’au lieu d’un simple son apparaît tout une figure, alors cette dernière morphologie viendra peu à peu supplanter celle de la structure. Il ne faut pas oublier que, dans ce dispositif, la structure (comme les matrices de Markov ici) est une information de transposition pour un son échantillonné. Voici quelques exemples dans lesquels les sons de références sont des objets composites et complexes, qui aideront mieux à faire comprendre cette situation. Voici d’abord un arpège échantillonné :
Et voici maintenant la structure (la partition) sur laquelle cet arpège va être transposé, qui est à sa manière une sorte d’arpège plus lent :
Nous obtenons donc, comme résultat, un arpège d’arpèges :
Voici maintenant un exemple plus complexe. Ici nous avons une structure composée de plusieurs accords qui servira à la fois de son de référence et de partition :
C’est-à-dire que chacune des notes de cette structure sera le prétexte à sa propre transposition. Ainsi, lors du première accord de 3 sons, nous obtiendrons 3 transpositions différentes de cette même structure avec le fait, bien connu des utilisateurs d’échantillonneurs, que plus une transposition est grave, plus son tempo sera lent, plus elle sera aiguë, plus son tempo sera rapide. Le résultat sera une séquence complexe dans laquelle nous ne reconnaîtrons aucune des notes la composant, la seule forme qui survivra à cette transformation sera son enveloppe générale. On entend encore une évolution du medium vers l’aigu et une petite redescente à la fin. La perception formelle est ici placée sur un terrain de la globalité, le détail étant noyé par une accumulation de formes intriquées les unes dans les autres :
6 – La réécriture des hauteurs et des durées.
Dans une autre section de Pluton, j’ai utilisé ce procédé des matrices de Markov dans un contexte assez différent. Les matrices ne reproduisant que ce qui a été joué, il s’ensuit que la musique qui en provient est très proche de celle qui en a été l’origine. On peut dire que, ainsi utilisées, les matrices de Markov constituent un double infini de ce que joue l’instrumentiste soliste. J’ai cependant voulu créer des formes qui, bien qu’elles prennent toujours leurs sources dans le même jeu du soliste, s’éloignent un peu du modèle, en tout cas n’en poursuivent que certains aspects. En voici un exemple dans lequel seule l’ossature rythmique est conservée, mais plus les hauteurs. Ici la matrice prendra sa source sur une « toccata » basée sur un « mi bémol » central du piano et se développera au fur et à mesure que le piano enverra de nouvelles informations à l’ordinateur en remplissant peu à peu la matrice de Markov, créant du même coup de nouvelles transitions entre les notes :
La matrice déroulera cette « toccata » de façon autonome et pratiquement infinie car le système trouvera tout le temps au moins une succession pour chaque note exprimée[5]. Après avoir fait franchir à ces matrices plusieurs étapes, j’ai décidé de les réduire à leur seul squelette rythmique en compressant toutes les valeurs de hauteurs sur un simple unisson. Ce procédé est un peu équivalent à celui qui consisterait à concentrer tout un clavier de piano sur une seule et unique note centrale, voire le réduire ou l’étendre au delà de ses limites habituelles. Voici donc l’effet que produit cette réécriture des hauteurs qui, avant d’arriver sur le « mib » central passent par des échelles compressées en micro-intervalles :
Vers la fin du processus l’ambitus revient progressivement à sa valeur originale (la gamme chromatique tempérée) en passant par des transitions de micro-intervalles :
Mais la plus radicale des transformations est donnée par la réécriture de la structure des durées. J’ai déjà expliqué que lorsqu’une transition entre deux notes est rejouée, la première transition est effacée par la seconde. C’est ainsi que j’ai eu l’idée de « verticaliser » progressivement toute cette toccata. Voici un exemple simple de ce fonctionnement. Lorsque je propose une succession mélodique telle que :
chaque note est soumise à un temps de transition qui sera respecté à chaque fois qu’elle celle-ci s’effectuera. Si maintenant je condense chacune de ces notes en un accord, j’efface tous ces temps en les ramenant à un temps zéro :
Le groupe {do, ré, fa} se reproduira chaque fois qu’une de ces trois notes aura été choisie comme successeur d’une précédente, et quelle que soit cette note parmi les trois, c’est en groupes qu’elle seront désormais produite. Le groupe {sol, lab} provient dans ce contexte de la transition {fa->lab} dans l’exemple mélodique précédent, et comme le sol a été maintenant ramené au même temps que le lab, il se produira également tout le temps que le lab aura été choisi. C’est ainsi que lors de la fin de cette « toccata », je lui fais subir une destruction progressive par l’annulation de ces composants mélodiques. En prenant toutes les notes de la séquence qui a servi de modèle à la « toccata » et les regroupant en accords, je produis un effet de contraction rythmique remarquable dans son comportement. Bien qu’il subsiste toujours quelques bribes de mélodies, l’ensemble suit la tendance à se verticaliser en grands accords. Certes, dépendant de tirages probabilistes, le résultat sera toujours différent. La verticalisation interviendra parfois un peu plus tôt, parfois un peu plus tard. Mais la tendance sera la même. Le pianiste, ici, a d’ailleurs la possibilité de rejouer plusieurs fois les accords jusqu’à obtenir une musique pratiquement toute verticalisée, où ne subsistent que quelques rares moments mélodiques :
L’expérience a prouvé que lors de très nombreuses interprétations de cette œuvre, ce passage a toujours été le plus surprenant par son comportement anarchique. La tendance est à la verticalisation progressive, mais on ne sait jamais à quelle vitesse celle-ci va s’accomplir. Dans ce cas particulier, plus le pianiste répètera ces accords plus il forcera cette toccata à se bloquer sur de grands agrégats jusqu’au moment ou il s’apercevra que la probabilité d’obtenir encore quelques bribes mélodiques est devenue tellement faible, que le moment est venu de clore cette section et de passer à la suivante. Il en résulte un dramatisme très particulier, qui est propre à la musique en temps réel, et qui n’existe dans aucune autre sorte de musique. Les musique écrites ou les musiques électroniques sur un support fixe reproduisent, dans les grandes lignes, toujours les mêmes proportions, et la musique improvisée est incapable de gérer des processus aussi complexes. Il n’y a que dans les situations de temps réel interactif que l’on peut avoir ce genre de « challenge » où l’on connaît le chemin mais ignore le temps qu’il va nous falloir pour le parcourir. Tout le suspens réside dans ce mélange de certitude et d’incertitude, dans cette relation entre notre capacité à prévoir le futur et notre étonnement, lorsque cette capacité est battue en brèche..
7 – Filtrage des durées : comment passer d’un discours discontinu à continu ?
Dans une autre composition, La partition du Ciel et de l’Enfer, j’ai également utilisé ce procédé des matrices de Markov en y effectuant un contrôle sur les durées. Ce genre de procédé fait partie d’une catégorie très importante dans les techniques de composition en temps réel : les critères sélectifs. L’analyse de l’interprétation peut se faire avec l’établissement de seuils, ou de fenêtres d’observation qui ne laissent passer qu’une partie des données produites par l’interprète. Dans ce cas, la différence entre la séquence-modèle et sa conséquence aléatoire, via les matrices de Markov, sera marquante. Autant la partition du jeu instrumental sera discontinue et abrupte, autant la « réponse » markovienne sera continue. Il suffit pour cela de mettre un seuil dans l’acceptation des durées de transition de note à note. Ainsi, lors de l’exécution d’une séquence rythmique telle que celle-ci
(Pianos: Pierre-Laurent Aimard et Florent Boffard. EIC : direction Pierre Boulez)
il faudra établir une limite de temps au dessous de laquelle les transitions ne sont pas prises en compte. Si cette limite est fixée sur une valeur très basse, par exemple de l’ordre de 300 ms, seules seront prises en compte les transitions se situant en dessous et, donc, le résultat de cette reproduction markovienne donnera une sorte de continuum ne reproduisant que les transitions exprimées en triples croches et n’inclura pas les valeurs de points d’orgues plus longues :
8 – Transitions et interférences d’arpèges et d’accords : aux limites de l’informel.
Dans une composition plus récente, Le temps, mode d’emploi pour 2 pianos et électronique en temps réel, j’ai utilisé à nouveau ce processus des matrices de Markov. Je me suis particulièrement attaché à m’en servir dans le but de traiter des formes tout à fait reconnaissables, voire des archétypes, et à en étudier les interférences qu’elle peuvent avoir les unes sur les autres. Le début de ce processus est exposé par les deux pianos sous forme d’une suite d’accords de 7 à 8 sons donnant naissance à 4 matrices superposées[6]. Le résultat donnera une déflagration d’accords dérivés de toutes ces successions :
(Pianos solos : Andreas Grau et Götz Schumacher)
On peut ici entendre la partie électronique seule sans la participation des 2 pianos solistes :
Évidemment les transitions qui peuvent exister entre deux accords concernent toutes les notes. Par exemple, la succession de ces 2 accords de 4 sons portera à 16 le nombre de probabilités différentes grâce auxquelles ils pourront se reproduire :
Quelques instants après intervient une autre forme tout aussi reconnaissable que ces accords : l’arpège. Deux arpèges surgissent ici qui vont interférer avec les accords :
Voici comment ces deux arpèges, introduits au milieu de ces déflagrations d’accords vont interférer avec ces derniers dans la musique électronique, grâce aux chemins empruntés par les matrices de Markov. On y entend très clairement des bribes mélodiques très rapides, sortes de résidus d’arpèges qui viennent s’insérer entre les groupes d’accords :
Bien sûr, ces arpèges doivent posséder des notes communes avec les accords. Lors du tirage aléatoire, la matrice choisit la note suivante ; si celle-ci fait partie d’un arpège, alors la succession de l’arpège est confirmée pour un instant, si elle fait partie d’un accord, c’est cette forme qui est choisie :
De ce fait, nous obtenons des formes intermédiaires dans lesquelles des bribes d’accords ses disputent avec des lambeaux d’arpèges. Les textures qui se créent dans ce contexte musical peuvent aller jusqu’aux limites de l’informel. Dans ce cadre, l’informel naît de l’excroissance du formel. Rien d’autre n’existe que ces formes répertoriées que sont les accords et les arpèges. Pas de figures plus complexes ou ambiguës, mais des interférences de plus en plus rapides qui finissent par créer un brouillage sonore. La découverte de ces délires texturaux m’a tout de suite fait penser à des équivalents visuels qu’on trouve dans les surfaces très chargées des tableaux de Jackson Pollock, ou dans certains autres de Gerhard Richter.

Voici un exemple dans lequel le système est poussé jusqu’à son paroxysme. Ici la différence entre les deux formes de base (accord et arpège) s’estompe par le fait que les notes qui les jouent sont de plus en plus courtes et atomisées. Les accords perdent leurs résonnances et ne sont que des agrégats très brefs. Ici les textures sont de plus en plus violentes :
Il est important de souligner un détail d’ordre général. Un algorithme de composition, ou de génération aléatoire comme c’est ici le cas, n’a vraiment d’intérêt compositionnel que s’il se prête à des transformations puissantes et non à de simples imitations. Il est toujours important, dans l’écriture de telles procédures informatiques, de prévoir un assez grand nombre de paramètres pouvant faire varier les résultats de façon à obtenir des expressions musicales riches et diverses. C’est grandement de quoi il va être question dans la seconde partie de ce texte portant sur une utilisation différente des matrices de Markov.
9 – Comment inverser la courbe proliférante des matrices de Markov ?
Une des particularités de ces procédés de générations aléatoires, basés sur les successions de notes à notes, est qu’ils se comportent tout le temps par accumulation. On accumule différentes séquences qui interfèrent les unes avec les autres, et le système évolue toujours dans le sens d’une prolifération et d’un accroissement de la complexité texturale. Je me suis toujours demandé comment il serait possible d’obtenir des matrices négatives et, jusqu’à présent, je n’ai pas encore trouvé de résultat satisfaisant. Cependant, j’ai utilisé un procédé de filtrage qui parvient à peu près, et de manière très simple, au même résultat. Il consiste à dresser une liste de notes qui seront éliminées avant d’être synthétisées. Dans Le temps, mode d’emploi j’ai utilisé ce procédé pour opérer un filtrage progressif de toute une structure musicale jusqu’à la réduire à une seule note. Voici la structure de base avec toutes les hauteurs qui la constituent. Elle repose sur un ensemble de hauteurs dont chacune entretien une probabilité de succession avec toutes les autres. Comme ce procédé est ici multiplié sur 4 couches, cela donne des distributions de ces mêmes hauteurs dans des ordres différents. Le résultat sonore n’est, ni plus ni moins, ce que l’on appelle une hétérophonie :
Voici maintenant la même séquence, mais avec les deux pianos solistes qui, eux aussi, reproduisent ces éléments hétérophoniques :
Quelques mesures plus loin, le processus continue de se dérouler mais avec des filtrages. Seules les notes figurant entre parenthèses dans la partie électronique de l’exemple ci-dessous seront jouées. La manière dont ce filtrage est réalisé est extrêmement simple : dès qu’une hauteur n’appartient pas au groupe sélectionné, son amplitude est mises à 0 :
Voici ici une étape plus avancée de ce filtrage : seules 6 notes échappent aux filtres :
Et pour terminer, les deux séquences finales où ne subsistent respectivement que deux et une seule note :
10 – Smerdiakov : un autre modèle, ou comment fabriquer de la synthèse sonore markovienne ?
Voici un modèle différent de l’utilisation des chaînes de Markov pour engendrer des séquences musicales. Ce modèle, dû à l’ingéniosité imaginative de Miller Puckette, m’a servi dans de nombreux cas[7]. Je montrerai deux exemples de ce nouveau principe de distribution sonore. Les valeurs composant les matrices, ici, ne sont pas prises en temps réel dans le jeu d’un interprète mais sont données comme des paramètres. Parmi celles-ci, les valeurs de temps qui sont contrôlées par un métronome dont la vitesse peut varier. Dans le premier exemple, les chemins markoviens sont utilisés pour les besoins de la synthèse de sons. Il s’agit d’un modèle inventé par Miller Puckette alors que je lui demandais s’il était possible de trouver une méthode pour que les paramètres principaux pour construire des spectres soient extraits de l’analyse du son instrumental[8]. Ici, il n’y a pas d’analyse du son instrumental, mais uniquement de la synthèse pure. Voici ce modèle brièvement décrit.
Le modèle est basé sur 3 fréquences (je lui ai donné le nom de synthèse 3F) qui, par leurs relations harmoniques, vont construire des spectres le plus souvent inharmoniques. Comme les fréquences de ces spectres dont calculées en effectuant les sommes et les différences de ces 3 fréquences dans toutes leurs combinaisons possibles, il est normal de trouver, lorsque ces fréquences sont à l’unisson ou à l’octave, des spectres harmoniques, puisque 100 + 100 + 100 + 100… donnent 100, 200, 300, 400… comme 200 -100 = 100, 300 -200 = 100, 400 – 200 = 200, etc. Lorsque les fréquences ne sont pas égales ou à l’octave, les spectres sont plus ou moins teintés d’inharmonicité suivant la complexité des relations intervalliques de ces fréquences de base. Un des intérêt de ce type de synthèse est qu’il permet d’obtenir une grande variété de spectres différents à partir des mêmes fréquences de bases suivant que l’on va chercher les fréquences ainsi obtenues par additions et soustractions dans des régions plus ou moins éloignées dans l’aigu, dans des ambitus plus ou moins serrés ou étendus. Voici, à titre d’exemple, une série de spectres obtenus à partir de 3 fréquences qui, pour la démonstration, sont toutes accordées suivant l’accord parfait de do majeur : do, mi et sol. On entend ici très clairement cet accord à l’intérieur de tous ces spectres inharmoniques :
Et les matrices de Markov dans tout cela ? Elles vont servir à faire se promener une des trois fréquences pendant que les deux autres seront accordées fixement. Ainsi sur les 3 fréquences A, B et C, nous aurons A qui obéira à une distribution de type markovien pendant que B et C seront figées sur des hauteurs fixes. La vitesse de déroulement de ces spectres est donnée par un métronome :
Pour que ces matrices fonctionnent, elles doivent prendre des informations dans un fichier qui remplit, à certains égards, le rôle qui était celui de l’analyse instrumentale dans les exemples précédents : il fournit une série de paramètres. Voici un exemple de ces paramètres :
69 204 1843 57 57
Le premier chiffre (en partant de la gauche) représente le pitch en notation Midi, le second est le temps (en ms) depuis le pitch qui a été donné précédemment, le troisième est la durée, le quatrième est la probabilité d’apparition de ce pitch et le dernier sa vélocité (ou intensité). Ce sont surtout le premier et l’avant-dernier chiffres qui nous intéressent car ce sont eux qui créeront les chemins entre les hauteurs. Voici maintenant une liste dans laquelle on peut lire les probabilités de successions. On peut y lire que le « la » (69) à 47% de probabilité d’être suivi par un « sol# » (56) et, quelques lignes plus loin, 54% par un « sib » (58) :
58 0 3125 42 56
69 204 1843 57 53
56 697 1631 47 49
61 777 1380 48 58
50 182 1318 45 49
47 1015 3740 52 50
69 105 567 66 68
58 494 292 54 44
60 709 718 59 63
58 130 1484 45 58
61 562 141 59 62
Mais comme on va le voir maintenant, à partir de ces réseaux de transition, ce modèle dispose de beaucoup de paramètres permettant des variations importantes sur les résultats. La première de ces variations concerne à la fois le tempo et les valeurs de durées. Voici un petit exemple dans lequel nous entendons une distribution rythmiquement régulière (comme s’il s’agissait d’un métronome), mais partant d’une très grande vitesse pour arriver à une très grande lenteur :
Dans un tempo fixe, un autre paramètre fera varier les différences de durées séparant les transitions entre les hauteurs successives. On peut, de façon continue, partir des durées initiales (celles exprimées dans la liste ci-dessus par exemple) et, petit à petit, les rassembler sur une durée unique, une moyenne commune à toutes ces transitions. C’est ce qui se passe dans l’exemple suivant :
D’autres types de transformations sont également possibles dans le domaine des hauteurs. Lors d’une distribution de type markovien, ce sont évidemment les chemins entre les hauteurs bien précises qui sont concernés. Il est toutefois possible de transposer globalement et dynamiquement ces successions de hauteurs de l’extrême grave à l’extrême aigu. Ainsi chacune des notes de ces chemins markoviens peut être transposée sur un intervalle différent lorsqu’on fait glisser l’indice de transposition en continu d’un point à un autre. Le résultat e