La synthèse 3F.
Les sons de synthèse utilisés dans Das Wohlpreparierte Klavier proviennent d’un algorithme que Miller Puckette a mis au point pour moi en 2006 et que j’ai utilisé depuis dans la plupart de mes compositions avec électronique. Ce modèle de synthèse est basé sur un calcul de spectre sonore à partir de 3 fréquences de bases, et c’est pour cette raison que je lui ai donné le nom de « Synthèse 3F » . Je ne vais parler ici que de l’engendrement des fréquences et non pas de leurs courbes d’amplitude et autres attributs sonores. Le calcul des fréquences. L’idée de base est la suivante. On prend 3 fréquences f, g et h et on prend toutes les sommes possibles de toutes des fréquences f, 2f, 3f, 4f… avec g (2g, 3g…) et h (2h, 3h…)
f 2f 3f 4f….
g (f+g) (2f+g) (3f+g) (4f+g)…
2g (f+2g) (2f+2g) (3f+2g) (4f+2g)…
h (f+h) (2f+h) (3f+h) (4f+h)…
(g+h) (f+g+h) (2f+g+h) (3f+g+h) (4f+g+h)…
(2g+h) (f+2g+h) (2f+2g+h) (3f+2g+h) (4f+2g+h)…
…
2h (f+2h) (2f+2h) (3f+2h) (4f+2h)…
(g+2h) (f+g+2h) (2f+g+2h) (3f+g+2h) (4f+ g+2h)…
(2g+2h) (f+2g+2h) (2f+2g+2h) (3f+2g+2h) (4f+2g+2h)…
On prend ensuite les résultats de toutes les différences entre ces ensembles mais, pour éviter une trop grande densité, on ne prendra que les valeurs absolues de ces calculs ce qui donne :
1: f g h 2: 2f (f+g) (f-g) (f+h) (f-h) 2g (g+h) (g-h) 2h 3: 3f (2f+g) (2f-g) (2f+h) (2f-h) (f+2g) (f+g+h) (f+g-h) (f+2h) (f-2h) (f-g+h) (f-g-h)3g (2g+h) (2g-h) (g+2h) (g-2h) 3h
3.2.2 La répartition des fréquences suivant un indice de probabilité. Ensuite intervient un paramètre de probabilité qui, lorsqu’il est à 1 donne les premières fréquences du spectre. Par exemple si nous voulons 6 fréquences ce sera les 6 premières fréquences du spectre qui seront sélectionnées :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28…
Lorsqu’on descend l’indice de probabilité, les 6 fréquences seront choisies aléatoirement dans un ambitus plus large :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28…
Si on le baisse encre, on ira chercher des fréquences encore plus éloignées :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28…
Et ainsi de suite :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28…
Voilà pour les principes généraux. Quelles sont maintenant les spécificités musicales que l’on peut tirer d’un tel système ? Harmonicité et inharmonicité Il me semble qu’un des premiers avantages de ce type de spectre est qu’il permet de relier les dimensions harmoniques et inharmoniques dans un même objet. Je vais m’expliquer en donnant des exemples sonores. Dans le cas suivant les 3 fréquences de base choisies pour le calcul des spectres sont (en notation MIDI) : 72, 76 et 79. On reconnaît ici les 3 notes formant un accord de Do majeur, choisies ici à dessein pour que l’oreille puisse bien l’identifier. Avec un indice de probabilité à 1 et un choix de 16 fréquences, ce seront les 16 premières fréquences du spectre qui sera ainsi calculé et tous les sons seront donc identiques :
L’exemple suivant montre le résultat avec un indice de probabilité à 0.6 suivant lequel on entendra toujours la même famille harmonique (Do majeur) mais on percevra nettement que ces spectres ne sont plus identiques, certains faisant résonner des partiels qui n’appartiennent pas aux autres :
En continuant de baisser cet indice (ici à 0.16), nous obtenons des spectres de plus en plus différents les uns des autres, mais toujours avec cette toile de fond construite à partir de l’accord de Do majeur :
Enfin, l’indice étant ici à son minimum (0), les spectres seront très différents les uns des autres et la teneur en inharmonicité ici finira par détruire presque complètement les bases harmoniques choisies au départ. Celle-ci se laissant juste deviner comme en filigrane. Je ne change rien aux 3 fréquences, c’est uniquement la répartition aléatoire des fréquences spectrales dans des régions très éloignées, due à la baisse de l’indice de probabilité, qui est responsable de ce phénomène :
Voici maintenant un balayage rapide de spectres dont les bases sont accordées sur les notes La et Mi :
La synthèse 3F accordée sur des intervalles naturels. Regardons ici une particularité de ce mode de synthèse. J’ai montré comment un accord parfait pouvait être « inharmonisé » jusqu’à se détruire presque complètement. Il me faut préciser ici que les notes choisies étaient toutes prélevées sur l’échelle tempérée en demi-tons égaux. Le résultat sera assez différent si, au lieu de choisir des intervalles tempérés, nous choisissons des intervalles naturels, c’est-à-dire des tierces et des quintes acoustiquement justes. Voici d’abird un premier exemple avec un accord de La majeur « tempéré » (c’est-à-dire en notation Midi 69, 73 et 76) balayé par la synthèse 3F. On entendra ici, comme dans l’exemple précédent, un fort degré d’inharmonicité :
Maintenant si nous accordons ces trois fréquences en intervalles naturels, ce qui donnera 69, 73.8631 et 76.0195, nous entendrons nettement que la teneur en inharmonicité sera beaucoup plus faible et que le sentiment de « consonance » en sortira renforcé :
Le balayage par les chaines de Markov. C’est ici que l’utilisation des échelles prend tout son sens. Lors de la production des sons de synthèse par le modèle 3F, la première des trois fréquences se promènera sur les notes des échelles calculées, tandis que les deux autres resteront fixes pendant la durée des diverses séquences. La manière dont les fréquences de ces échelles seront choisies suivra le modèle des chaînes de Markov. Voici, pour commencer, un exemple simple dans lequel les échelles seront modifiées toutes les 4 secondes et soumises à un balayage continu et rapide avec les probabilités de successions entre les pas de ces échelles contrôlées par les chaînes de Markov. Pour que le phénomène soit bien saisi, j’ai volontairement accordé les 3 fréquences de la synthèse 3F à l’unisson, et limité le nombre de partiels des specrtes à 3, ce qui a pour effet que nous entendrons une seule note par specrtre, la fondamentale qui viendra se poser sur les notes de l’échelle en cours. Dans cette séquence, qui n’a pas de valeur musicale réelle, les échelles parcourues seront successivement celles-ci : 



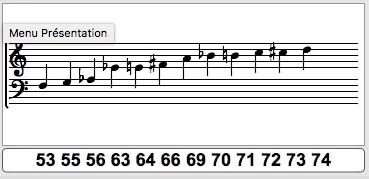




Comment construire des textures fluides à partir d’un système rigoureux. J’ai précisé, plus haut, que cette exemple n’avait pas de valeur musicale. Mais il m’importe maintenant de montrer que, comme pour la musique écrite, les esquisses sont autant de pas que l’on fait pour parvenir à une expression musicale valable. Certaines fois, les prémisses ne paraissent guère encouragantes, mais, comme un sculteur taillerait un bloc de pierre informe pour en dégager une figure, les compositeurs parviennent à dégager une expression sonore à partir d’un matériau qui, au départ, peut être brut et mécanique. C’est le cas ici. Je vais montrer qu’avec des modifications successives, je vais parvenir à faire émerger une structure musicale qui aura perdu tout ce qui fait le mécanisme très primaire qui était celui de l’exemple précédent. Je veux insister sur le fait que je ne changerai absolument rien des promenades markoviennes sur les échelles successives, mais que je modifierai par petites touches les éléments qui définissent les sons de synthèse. Pour imager ce procédé, je diriai que le processus de composition restera le même quand les détails de l’orchestration et de la mise en forme eux, varieront. La première modification sera un nouvel accordage des 3 fréquences de base de la synthèse 3F. Ils étaient à l’unisson précédemment, ici il vont être accordés sur des tierces majeures successives. Un paramètre appelé « offset » permet de transposer les notes de la première fréquences à des intervalles précis. Ainsi, lorsque la première fréquence donnera 60, j’ajouerai 4 pour la deuxième et 9 pour la troisième, et j’obtiendrai donc un balayage des échelles avec des accords de quintes augmentés successifs et parallèles. Et pour donner un peu plus de brillance aux sons j’ai poussé le nombre de fréquences maximum pour chaque spectre à 13, ce qui aura pour effet de produire des harmoniques plus aiguës :
Contrôle du contenu spectral avec l’indice de probabilité. L’ajustement suivant consistera à modifier graduellement le paramètre de probabilité qui, je le rappelle, permet d’obtenir des spectres plus diversifiés car, plus la valeur de probabilité sera basse, plus le choix des partiels pour être différend et atteindre des régions plus aiguës. Dans cet exemple, le paramètre de probabilité commence à 100, c’est-à-dire que pour un nombre fréquences maximum de 13 partiels, nous aurons les 13 premières fréquences calculées, à savoir la trasnposition des mêmes intervalles sur chacune des notes choises par les chîanes de Markov sur les échelles. A mesure que la séquence se déroule, l’indice de probabilité ira en diminuant et nous obtiendrons des spectres de plus en plus différents en ambitus et en contenus intervalliques :
Variation des amplitudes relatives à chaque partiels des spectres. On ne peut pas dire que, jusqu’à présent, la qualité et l’intérêt musical aient véritablement progressé. Mais le pas suivant nous conduit vers ce que l’on peut appeler un progrès dans l’expression. Car, qu’est-ce qui gêne dans les exemples précédents ? À mon goût, il demeure encore trop de régularité et le côté mécanique, s’il a été un peu atténué, n’a pas encore disapru. Une caractéristique est responsable de cela : toutes les amplitudes de chacuns des spectres calculés sont pratiquement égales. C’est-à-dire que tous les partiels sont ramenés à la même valeur et nous obtenons une série de spectres plats. En baissant progressivement le paramètre « ampJitter » j’obtiens une distribution aléatoire des amplitudes respectives pour chaque sons, favorisant ainsi une plus grande variété et, du même coup, réduisant de façon assez nette ce sentiment « mécanique » qui était celui des exemples précédents : 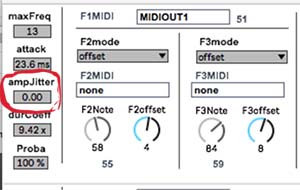
3.4.3 Modification et variation des durées des sons. Je vais maintenant faire un pas plus décisif dans la direction d’une recherche d’une plus grande variété sonore, puisque c’est cela, finalement, qui est à la base de tout ce processus. Deux éléments vont m’y aider. Après avoir différencier les contenus spectraux et les amplitudes relatives de chacuns des partiels les composants, c’est au domaine des durées des sons que je vais m’attaquer. En augmentant le coefficient des durées je vais obtenir des sons dont les temps de résonnance seront choisis dans une palette beaucoup plus large et non plus égales comme c’était le cas précédemment : 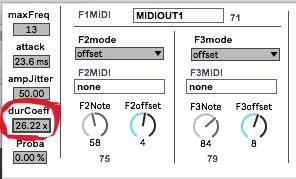 3.4.4 Irrégularité rythmique obtenue par filtrage Enfin, une autre modification va être apportée dans les amplitudes globales des sons. Jusuqu’à présent la « vélocités » de chacun d’eux étaient fixés au maximum, c’est à dire la valeur de 127 (puisque nous parlons ici en notation MIDI). En baissant la valeurs minimum à 0 et laissant la valeur maximum à 127 j’obtiendrai un distribution aléatoire choisie entre ces deux bornes. Ce tratement aura également un effet intéressant de filtrage car, au lieu d’avoir ce déroulement rythmique très mécanique, j’aurai ici des « trous » et des sons d’intensités différentes :
3.4.4 Irrégularité rythmique obtenue par filtrage Enfin, une autre modification va être apportée dans les amplitudes globales des sons. Jusuqu’à présent la « vélocités » de chacun d’eux étaient fixés au maximum, c’est à dire la valeur de 127 (puisque nous parlons ici en notation MIDI). En baissant la valeurs minimum à 0 et laissant la valeur maximum à 127 j’obtiendrai un distribution aléatoire choisie entre ces deux bornes. Ce tratement aura également un effet intéressant de filtrage car, au lieu d’avoir ce déroulement rythmique très mécanique, j’aurai ici des « trous » et des sons d’intensités différentes : 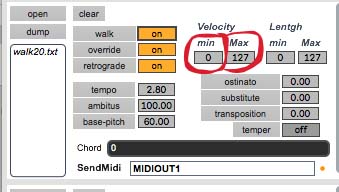
3.4.5 Décalage du spectre Un dernier arrangement consistera à donner une couleur différente aux sons avec un procédé très simple : le sons sera entendu tel qu’en lui même et aussi transposé. En le décalant soit vers l’aigu, soit vers le grave, on double les fréquences du spectre. J’ai choisi ici une transposition à la quarte augmentée (c’est à dire 6 demi-tons plus haut que l’original) : 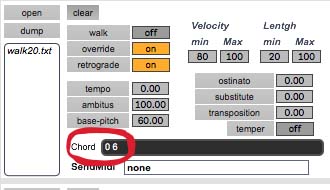 Et voici le résultat final :
Et voici le résultat final :
3.4.6 Exercice de « déconstruction » musicale. Par ces différents réglages de paramètres j’ai réussi, en partant d’une esquisse mécanique et très systématique, à créer une texture d’une grande fluidité qui semble se renouveler en permanence. Ce mode de fonctionnement est très important pour moi. Dans la plupart de mes compositions je me suis attaché à suivre une logique que je voulais la plus solide possible, parfois à la limite de la sévérité. Mais c’est dans les agencements des détails que je parviens à créer les conditions d’une écoute sensible sans, ceci dit, que la logique en soit brisée. Je vois dans cette manière de composer l’expression de la dialectique entre rigueur et liberté que j’ai tant apprécié chez bon nombre de compositeurs du passé. Et pour apporter une démonstration finale de ces différents processus et surtout une preuve que tout ce que j’ai présenté a été fait sans le moindre montage, qu’il s’agit bien de processus différents fonctionnant en temps réel, voici un dernier exemple qui remontera l’ensemble des processus en arrière. Je partirai cette fois du résultat final pour arriver à la première mouture. En d’autres termes, je déconstruirai pas à pas la structure finale pour retrouver l’esquisse première :