Le phénomène d’attraction sonore est un des thème de cette pièce. On le verra par la suite. L’idée qu’une voix, ou même une structure, subisse l’attraction d’une autre me semble être un des enjeux le plus passionnants de la musique à notre époque. Je vais m’en servir pour les mouvements spatiaux plus tard, mais ici il s’agit d’une attraction spectrale. Une voix se rapproche progressivement d’une autre par son comportement. Une fois que les paramètres de l’une sont identiques à ceux de l’autre, il est presqu’impossible de les distinguer. C’est ce qui se passe dans cet événement :
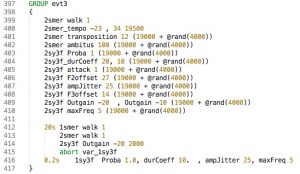
Le tempo, très lent au début (-23) s’accélère progressivement pour rejoindre celui de la voix 1 (34) pendant 19,5 secondes. Tous les autres paramètres (transposition, ambigus, Proba, etc.) vont également subir la même transition qui aboutira à la valeur correspondante dans la première voix. Pour ne pas égaliser toutes ces transitions je leur ai affecté une durée de base (19 secondes) à laquelle j’ai ajouté un nombre aléatoire compris entre 0′ et 4′ (19000 = @rand(4000)). Ainsi chaque paramètre calculera sa propre valeur aléatoire qui sera donc différente pour chacun.
Voici la première voix (tempo très rapide et aigu) :
puis la seconde avant la progression (tempo très lent et grave) :
et voici la progression de la seconde pour rejoindre la situation de la première :
Pour bien comprendre ce processus de synthèse, voici une présentation, paramètres après paramètres, de toutes ces transitions :
Voici, pour commencer, l’évolution conjointe de la durée des sons (de plus en plus courts) et du tempo (de plus en plus rapide) :
Maintenant, l’évolution des paramètres ampJitter et Proba, respectivement responsables de l’égalisation des amplitudes de chacun des partiels dans les spectres et de l’augmentation de la probabilité pour avoir des spectres répartis sur des ambitus contrastés :
Voici maintenant la transposition des fréquences F2offset et F3offset qui sont les fréquences 2 et 3 de la synthèse 3F qui partent de l’unisson (de ce fait, les sons graves donnent des spectres harmoniques avec des hauteurs bien repérables) pour aboutir à des transpositions de la fréquence 1 (elle, générée par le flux markovien) de 27 demi-tons pour F2offset et 14 demi-tons pour F3offset :
Jusqu’ici les mouvements de plus en plus chaotiques que l’on entendait étaient dus à la variabilité des spectres qui les composaient (Proba = 1). Les pitchs générés par le flux markovien qui contrôle la première fréquence de cette synthèse 3F (que l’on pourrait de façon un peu abusive appeler les fondamentales des spectres) étaient réduits à une simple note répétées. Voici maintenant la transposition de cette note répétée sur l’intervalle d’une octave au moyen d’un glissando :
Et, pour terminer, à partir de cet état sonore, je vais rajouter les derniers éléments qui sont l’augmentation de l’ambitus des chemins markoviens qui, partis de l’unisson, verront leurs intervalles s’agrandir peu à peu jusqu’à atteindre une échelle tempérée en demi-tons, puis une réduction du temps d’attaque à 1ms et une diminution du nombre partiels à 5 :
Je profite de ce petit exemple pour aborder un sujet important concernant la gestion temporelle des événements musicaux en temps réel. Une « partition informatique » telle que celle de Das Wohlprepärierte Clavier comporte plusieurs types de temporalité. Il existe des temporalité qui sont inscrites dans la partition. Ainsi lorsque j’écris : 2sy3f Proba 1 19000, je compose comme un peu comme sur une bande magnétique, c’est-à-dire que je définie une valeur absolue qui est notée « en dur » et ne changera pas: la variable Proba devra atteindre la valeur 1 après 19 secondes à partir du moment où cette action a lieu. Si maintenant j’écris : 2sy3f Proba 1 (19000 + @rand(4000)), j’introduis une valeur aléatoire qui s’ajoutera à ces 19 secondes et sera comprise entre 0 et 4 secondes. Même si cette durée n’est pas connue avant son exécution, elle quand même inscrite dans une certaine mesure dans la partition. Il n’en est pas de même lors que je fais se succéder deux événements par rapport à un suiveur de partition attachée à un interprète. Ainsi dans la partition suivante :
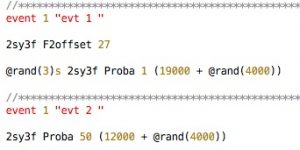
je fais ce succéder deux événements. L’événement 1 comporte 2 actions :
- 2sys3f F2offset 72 qui est une simple affectation.
- 2sy3f Proba 1 (19000 + @rand(4000)) où on retrouve la progression mentionne plus haut, mais ici précédée d’une commande : @rand(3)s.
Cette dernière instruction est un délai en secondes (la lettre « s » l’indique) dont la durée aléatoire est comprise entre 0 et 3. Cette action est donc une action retardée dont la valeur va être calculée au moment même de l’exécution.
L’événement 2 comporte la progressions 2sy3f Proba 50 (12000 + @rand(4000)) qui est attachée à la même variable que variable que précédemment: Proba, qui ira ici à 50 en 12 secondes (plus une valeur aléatoire).
Mais le moment où va intervenir l’événement 2 est inconnu car il dépend de l’interprète. L’événement 2 devrait suivre l’événement 1 après 26 secondes maximum (19 plus la valeur aléatoire maximum qui est de 4 secondes auquel il faut ajouter la valeur de délais maximum qui est 3), sinon la progression de la variable Proba n’aura toujours pas atteint son premier but (qui est de converger vers 1) qu’elle devra se diriger vers 50 lors de l’événement 2. Cette temporalité est tributaire de la situation musicale qui est celle du concert et qui veut qu’il serait illogique d’interrompre une progression avant sa fin. Cependant, pendant les répétitions, il serait fastidieux d’attendre ces 26 secondes à chaque fois que l’on répètera ce passage. Il nous faut donc mettre la variable Proba à 1 dès le début de l’événement 2 pour la faire aller vers 50. Ce n’est pas un problème car il suffit de réécrire cette instruction telle que : 2sy3f Proba 1, 50 (12000 + @rand(4000)) et on a définit ainsi les bornes de cette progression. Mais c’est sans compter avec le délai variable de l’événement précédent. Le programme Antescofo a fort heureusement pu traiter cette situation de la manière suivante :
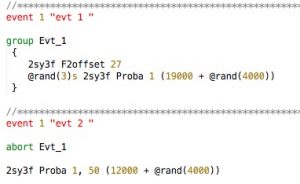
Lorsqu’on créé un group, compris entre deux {}, celui ci peut être « tué » par la commande abort, suivie du nom du group. En tuant ce « group » on tue également tous ses descendants, c’est -à-dire tous les processus auxquels il a donné naissance. L’informatique est décidément d’une grande cruauté ! Ainsi lors de la commande commande abort Evt_1 le délai de l’événement 1 cesse d’être calculé et la première progression de la variable Proba également. On peut donc aller directement à l’événement 2 sans attendre le temps d’exécution de l’événement 1.