éIl m’arrive souvent de dire que Tensio, pour quatuor à cordes et électronique en temps réel, représente l’œuvre la plus expérimentale que j’ai composée jusqu’à aujourd’hui. Il faudrait remonter aux débuts de mes travaux dans le domaine du temps réel dans les années 80, avec les compositions de Jupiter et de Pluton, pour trouver une aussi grande utilisation de techniques nouvelles et expérimentales dans l’élaboration et l’écriture des œuvres. Ce travail s’est fait grandement en collaboration avec Gilbert Nouno, qui a réalisé la partie informatique et mis au point une grande partie de ces nouvelles techniques, et Arshia Cont, dont les dernières recherches ont grandement influencées cette composition. La contribution de Miller Puckette a aussi été décisive dans certains domaines comme celui de nouveaux procédés de synthèse sonore. J’aborderai dans ce texte ces nouveaux outils de synthèse qui sont à la base d’une grande partie de ce quatuor, mais aussi des points de vues plus théoriques quant à leurs relations avec l’écriture instrumentale.
1) Les outils de synthèse utilisés dans Tensio.
Trois modèles de synthèse sont utilisés dans Tensio. Ils vont du plus classique au plus abstrait. La musique électronique qui répond au quatuor à cordes sera tour à tour, proche ou lointaine, familière ou inconnue. Il m’a fallu créer parfois un quatuor virtuel qui dialogue avec le quatuor réel sur la scène, parfois un son de corde qui produit des musiques que ne pourraient pas produire les musiciens de ce quatuor et parfois, des configurations sonores totalement étrangères au monde du quatuor mais cependant dérivées de celui-ci. Dans leur ordre d’apparition dans l’œuvre, mais aussi dans leur ordre d’éloignement des sons réels du quatuor ; ces trois modèles sont : Synful, la synthèse par modélisation physique et la synthèse 3F.
a) La synthèse instrumentale par le programme Synful.
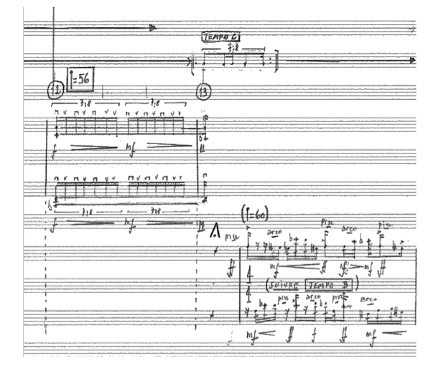
Le programme Synful, mis au point par Eric Lindemann, permet de recréer les sons instrumentaux de l’orchestre classique mais, à la différence des outils d’échantillonnage que l’on connaît sur le marché, ce programme ne prend pas seulement en compte le son lui-même mais sa transition avec le suivant. Il est possible, par exemple, de faire exécuter un vrai légato à une clarinette ou à un ensemble de violoncelles. L’ayant déjà utilise dans Partita I, ce modèle de synthèse m’a été d’une grande utilité pour Tensio, particulièrement pour créer un quatuor virtuel qui se superpose au quatuor réel. Je parle de quatuor virtuel pour bien indiquer que les sons qui seront produits se confondront sans problème avec les sons produits par les instrumentistes réels sur la scène. C’est en particulier ce qui se passe dans le tout début de l’œuvre, dans lequel on entend une structure très dense et polyphonique dont les éléments sont distribués à la fois dans le quatuor réel et dans le « quatuor Synful ». Trois couches sont superposées : des accords en trémolos, une succession de pizzicati répétés, ainsi que trois sons de « violon » en crescendo. Le tout étant soumis a des traitements en glissandi montants et descendants obtenus par un harmonizer :
Voici un autre exemple dans lequel le même matériau est utilisé, mais dans une autre organisation et de façon plus dense. On y retrouve les glissandi d’harmonizer, les pizzicati répétés, les trémolos et les sons crescendo le tout dans une forte dimension polyphonique :
Dans un tel environnement, lorsque la musique de synthèse est si proche de celle du quatuor, il n’y aucun problème pour la noter de façon traditionnelle sur partition. D’autant qu’ici, nous restons dans un contexte totalement déterministe dans lequel la plupart des valeurs sonores sont au préalablement fixées et connues à l’avance, à l’exception du moment exact où elles vont être jouées, celui-ci dépendant du suivi de partitions et donc du violon I. Ce ne sera plus le cas dans les deux autres modèles de synthèse utilisés qui, par leur nature propre et leur mode de fonctionnement, échappent à toute notation précise et prédéterminées.
b) La modélisation physique d’une corde de violon.
Lors de la composition de Partita 1 pour alto et électronique en 2009, mon souhait avait été d’utiliser un environnement de cordes artificielles dont le contrôle sonore aurait été assuré par le soliste lui-même. L’analyse de données sonores effectuées en temps réel pendant l’exécution devait avoir le pouvoir de modifier les comportements acoustiques de ces cordes artificielles. J’avais alors jeté mon dévolu sur la synthèse par modélisation physique. L’idée était séduisante mais totalement utopique à cette époque. Elle l’est encore partiellement de nos jours car les méthodes d’analyse sonores en temps réel sur les différents instruments restent encore embryonnaires quant à leurs véritables usages dans le domaine de la composition. D’autre part, les systèmes de synthèse par modélisation physiques existants à l’époque, n’auraient nécessités pas moins de quatre ordinateurs, un pour chaque corde artificielle ! Plus encore, ces systèmes s’avéraient pratiquement inutilisables dans le domaine compositionnel : la modification d’un des paramètres entrainait une trop grande déstabilisation de tout une série d’autres paramètres et donnait un aspect proprement chaotique et incontrôlable à l’ensemble. Comment un environnement complexe et puissant doit-il être organisé sous une forme efficace pour la composition ? C’est là une grande question qui mérite d’être soulevée. La composition, qu’elle soit sur partition écrite ou sur un système de synthèse sonore, demande une forme de simplification (d’abstraction) de son écriture pour que puisse s’élaborer des constructions évoluées. Un environnement où les interconnexions entre tous les niveaux tendent à la prolifération devient très rapidement « ingérable » pour un compositeur. C’est une des grandes différences qui sépare le monde de la composition de celui de la performance et de l’improvisation[1. Je me souviens d’une discussion que j’ai eue à ce sujet avec Don Buchla, un chercheur américain, original et célèbre à juste titre pour ses multiples inventions dans le domaine des synthétiseurs de sons. Il me disait que ses machines avaient du succès surtout car elles étaient imprévisibles, ce à quoi je lui répondis que l’imprévisibilité est aux antipodes du désir des compositeurs qui recherchent des expressions précises, tout au moins suffisamment précises pour qu’elles puissent se reproduire à l’identique. Les œuvres musicales ont une identité car on les reconnaît en ce qu’elles sonnent d’une manière bien particulière que l’on ne peut confondre avec une autre.]. J’ai décidé alors d’abandonner ce système de synthèse pour me consacrer à celui, plus classique en apparence mais tout aussi original, qu’a mis au point Eric Lindemann et connu sous le nom de Synful. Une fois la composition de Partita I achevée, on m’a montré un nouveau système de synthèse de corde par modélisation physique que venait de mettre au point Matthias Demoucron, un jeune chercheur français. Je trouvais qu’il arrivait un peu tard pour moi, mais c’est lui que j’ai finalement adopté lorsque j’ai décidé de me consacrer à la composition de Tensio.
La synthèse par modélisation physique est d’une toute autre approche que les autres modèles de synthèse existants en ce qu’on ne lui fournit pas des paramètres classiques, tels que les fréquences, les spectres ou les amplitudes, mais des modèles gestuels dont on dessine les évolutions dans le temps. Le système de Matthias Demoucron consiste en une modélisation d’une corde de violon tendue autour d’une caisse de résonnance, provenant de l’analyse d’un violon du XVIIème siècle. Ce modèle de corde, qui peut avoir des tensions différentes[2. C’est d’ailleurs une des origines du titre « Tensio », que j’ai choisi pour ce quatuor.] dont résultera sa hauteur, est excité par un archet virtuel dont on contrôle 4 paramètres : la force avec laquelle il frottera la corde, sa vitesse, sa position (sur le chevalet, sur la touche, ou entre les deux), et la hauteur (équivalente à la position d’un doigt de la main gauche sur la corde). Chacun de ces paramètres est accessible dans une fenêtre dans laquelle on dessine des évolutions temporelles. Dans l’exemple ci-dessous, on peut voir l’interface d’utilisation dans laquelle sont dessinées ces différentes évolutions temporelles.
a- les partie bleuâtre, commune à toutes les paramètres, détermine une fenêtre d’utilisation qui sera lue en boucle suivant un tempo déterminé.
b- La première fenêtre (s_force) montre la courbe d’évolution de la pression de l’archet au cours de la lecture de cette fenêtre. Cela correspond ici à un crescendo et un decrescendo.
c- La seconde fenêtre (s_vel) dessine les mouvements d’aller et retour de l’archet sur la corde, que l’on nomme dans le jargon musical : tiré-poussé.
d- La troisième fenêtre (s_dist) montre les évolutions de la position de l’archet : normale au début, évoluant vers le chevalet, puis vers la touche avant de revenir à la position médiane.
e- Enfin la fenêtre inférieure (s_pitch) montre une stabilité de la fréquence.
Les sliders qui se trouvent à la droite de ces fenêtres permettent un ajustement des valeurs dans des proportions plus infimes et précises que ne le propose le dessin des courbes :
Au cours des expérimentations que j’ai pu faire sur ce modèle, une chose m’a particulièrement frappée. Il s’agit de la combinaison de valeurs simultanées que ne pourrait pas reproduire avec autant d’exactitude un instrumentiste vivant. Plus particulièrement, la combinaison de mouvements qui seraient presque contraires à la nature physique d’un violoniste. Imaginons d’abord une situation classique. Pour produire un son faible, un violoniste va coordonner les mouvements de son bras et de sa main droite de manière à ce que la vitesse d’archet soit lente tandis que sa pression demeure faible. Au fur et à mesure qu’il voudra produire un crescendo, il va augmenter cette vitesse tout en accentuant la pression sur la corde. Ainsi un « beau son » (ce terme étant utilisé suivant les canons de la culture classique du violon occidental) ne pourra être produit que par de fréquents et allers-retours de l’archet sur toute sa longueur avec une vitesse assez rapide. La rapidité de ces allers-retours évitera que la forte pression qui est produite sur l’archet ne produise des aspérités sur le son. En effet, au fur et à mesure que l’on ralentira la vitesse de l’archet, le son aura tendance a devenir rugueux jusqu’à devenir grinçant et perdre toute sa caractéristique de hauteur au profit d’un son bruité[3. De tels effets font maintenant partie de la manière de jouer des violonistes contemporains, et des compositeurs comme Helmut Lachenmann, et dans une moindre mesure Gérard Grisey, se sont même fait une spécialité dans ce domaine. Le bruit jusqu’à la saturation est désormais accepté comme une potentialité expressive dans certaines esthétiques.]. Maintenant imaginons la situation suivante. Que se produirait-il si l’on continuait d’exercer une pression maximale sur la corde en ralentissant encore considérablement la vitesse l’archet jusqu’à une lenteur maximale ? Ce serait là une prouesse physique étonnante de la part d’un violoniste car plus on exerce un mouvement vertical du bras (pression vers le bas) moins on n’a le pouvoir de contrôler le mouvement horizontal (celui qui détermine la vitesse de l’archet). En d’autres termes, plus la pression sur l’archet sur la corde sera maximale et plus difficile sera de maintenir lisse et régulière sa vitesse. Or, on le sait, ce qu’un homme ne peut pas physiquement faire, une machine peut très bien s’en charger. Je fus alors très étonné d’entendre ce que produit cette action contre nature et de constater que la pression exagérée, contrairement à ce que l’on a pu observer dans la situation naturelle, ne fait plus tendre le son vers le bruit lorsque la vitesse tend vers la nullité et la régularité. Le résultat au contraire produit l’effet de petites gouttelettes sonores extrêmement aiguës, donnant l’idée de son perforé, mais dont les perforations seraient irrégulières. La fréquence variable de ses gouttelettes sonores est obtenue par de légères variations de la pression qui s’exerce continuellement dans un registre qui confine à l’écrasement de la corde par l’archet.
Afin de varier ce modèle et de le faire évoluer dans des registres expressifs différents, je l’ai transposé par des harmonizers afin de lui donner parfois des sonorités graves, qui évoquent quelques mystérieuses percussions de bois, et parfois dans des glissandi afin de le rendre plus mobile. Le grand intérêt que j’ai trouvé à ce modèle de synthèse réside principalement dans le fait que, bien que la modélisation des actions simultanées et contre nature des mouvements de l’archet produise des sons que l’on n’assimilerait pas directement avec ceux d’un violon, bien que la « physionomie » de ces sons tendent vers quelque chose d’inouï, en tout cas de non répertorié, il n’en demeure pas moins que l’on entend toujours que c’est une corde qui est actionnée. C’est un des grands principes sur lequel je base une partie de mon travail : ne pas détruire l’origine physique d’un son quand bien même celle-ci nous entraîne dans des régions fort éloignées du modèle initial. Il m’importait de trouver des sons nouveaux, mais il m’importait tout aussi bien de faire en sorte que l’auditeur ne perde jamais le lien, si ténu fut-il, avec ce qui constituait la base sonore de ce quatuor : une certaine tension exprimée sur une corde qui vibre.
c) « Inharmonisations » par la méthode de synthèse 3F
Depuis plusieurs années je caressais le rêve du pouvoir composer une musique électronique qui serait entièrement créée en temps réel et prendrait sa source dans le jeu instrumental. J’ai approché cette idée dans des œuvres telles que Jupiter, Pluton ou En écho, mais jamais de façon aussi avancées que dans Tensio. Ce qui est en jeu ici, c’est le problème du déterminisme et de l’indéterminisme en musique. Pour bien le cerner, il faut le préfacer en analysant ce que ces termes veulent bien signifier dans la pratique musicale. Observée sous une perspective très globale, une partition écrite est déterministe en ce que les éléments qui la constituent sont préalablement organisés par le compositeur sous une forme écrite indiquant les hauteurs, leurs niveaux dynamiques, leurs évolutions, et aussi leur temporalité. Or, tout le monde sait que ces partitions sont interprétées et que le propre de l’interprétation est de personnaliser une exécution à un moment donné. Donc il n’y a jamais deux interprétations identiques. Du point de vue de l’interprète, il existe toujours une marge de liberté à l’intérieur de laquelle il va pouvoir fixer ses intentions propres. Il s’agit cependant toujours d’intentions, qu’elles soient celles du compositeur ou de l’interprète, mais elles ne sont pas temporellement identiques. L’espace temporel de la composition n’est pas aussi « immédiat » que celui de l’interprète. La composition, si tant est qu’elle soit hautement élaborée, demande un temps de gestation, d’élaboration d’esquisses plus grand que celui de l’interprète. L’interprète, même le plus scrupuleux (prenons par exemple le pianiste Maurizio Pollini) peut « conditionner » sa vision de l’œuvre par l’analyse mais il ne peut physiquement pas prédire avec exactitude ce qu’il va produire. Le déterminisme (de la composition) et l’indéterminisme (de l’interprétation) se distingueront alors par le fait qu’il existe un écrit pour le premier et non pour le second. Vue sous un angle plus local, une partition recèle donc plusieurs niveaux d’indéterminisme, les principaux étant surtout les niveaux dynamiques et les flux temporels (Ces niveaux varient suivant les instruments car, bien entendu, un piano ne peut pas interpréter les hauteurs et leurs enchaînements avec la même finesse que, par exemple, un violon. On peut dire que, d’une manière générale, plus les instruments sont dotés de présences mécaniques (tels que le système des marteaux sur des cordes dans le piano) plus limitées sont ses possibilités d’interprétation.).
Cette séparation fondamentale entre ces niveaux déterministes et indéterministes, telle qu’on la trouve dans la musique instrumentale m’a servi de modèle pour ce que j’ai nommé, dans la musique électronique, les « partitions virtuelles ». J’en rappelle ici la définition : une partition virtuelle est une partition dont on connaît apriori les paramètres qui la constituent, mais pas la valeur exacte qu’il vont recevoir. Si on ne peut pas les connaître à l’avance c’est pour une raison très simple : ils vont être captés dans l’interprétation qui, comme on l’a vu, contient une grande marge d’indéterminisme. Il est cependant toujours possible de concevoir des systèmes qui comportent ces deux états, déterministe et indéterministe, car une partie des paramètres nécessaires à la création de sons de synthèse peuvent très bien être notés dans un programme tandis qu’une autre partie proviendra de l’analyse en temps réel d’un instrument au moment même de l’exécution musicale.
Lorsque j’entrepris la composition de Tensio, avec l’aide de Gilbert Nouno, j’ai expérimenté plusieurs modèles de synthèse qui pouvaient utiliser des analyses de divers aspects du son instrumental pour créer des spectres sonores variés dans leurs constitutions sonores. Mais tous les résultats que nous avions obtenus ne me donnaient pas entière satisfaction car il était très difficile de contrôler les qualités sonores précises de ces sons à partir d’une telle complexité et variabilité obtenues à partir de ces analyses. C’est finalement Miller Puckette, à qui j’avais parlé de ce problème, qui m’en apporta la solution. Il imagina un système de construction de spectres sonores à partir de trois fréquences de base auquel j’ai ensuite donné le nom de Synthèse 3F. En voici, de façon assez résumée, le principe. On choisit trois fréquences (f, g et h) à partir desquelles on va ensuite effectuées une grande série d’opérations (additions et soustractions) telles que :
1 : f g h
2 : 2f (2+g f-g) (f+h) (f-h) (2g) (g+h) (g-h) 2h
3: 3f (2f+g) (2f-g) (2f+h) (2f-h) (f+2g) (f+g+h) (f+g-h) (f+2h) (f-2h)
(f-g+h) (f-g-h) 3g (2g+h) (2g-h) (g+2h) (g-2h) 3h
…
La somme de toutes ces opérations donne un spectre d’une extrême densité pouvant comporter plus de 100 partiels. Une telle situation pose un problème de base pour la perception : plus la densité spectrale est élevée et moins ces spectres pourront se différencier les uns des autres. Le criblage massif de l’espace des fréquences est un peu à l’image des clusters que l’on n’arrive pas à regrouper en familles distinctes. Pour résoudre ce problème, Miller Puckette a proposé de choisir, suivant des critères précis, des sous-ensembles de ces fréquences en limitant ainsi leurs nombres dans les spectres. Si l’on fixe à l’avance le nombre de fréquences dans les spectres à une valeur fixe, disons 16, on applique alors un crible qui accepte ou rejette chacune des fréquences obtenues suivant une probabilité donnée. Lorsque l’indice de probabilité sera égal à 1, nous obtiendrons les 16 premières fréquences (les plus graves) et plus cet indice ira en diminuant, plus on ira chercher les fréquences dans des régions éloignées (en progressant vers l’aigu) jusqu’à ce que l’on obtienne les 16 fréquences désirées. Ce choix aléatoire est responsable de l’irrégularité avec lesquelles ces fréquences seront distribuées dans le spectre. Si la probabilité est au moins égale à 0.25, il y aura de fortes chances pour qu’un des voisins (f+g), (f+h), (g+h), (2f+g+h), (f+2g+h), (f+g+2h) soit présents ce qui donnera une différence fréquentielle soit de f, soit de g, soit de h, et par là, une prédominance d’une de ces trois fréquences sur les autres. Ainsi, lorsque nous aurons un indice de probabilité faible, chaque nouvelle opération donnera un spectre grandement différent à partir du même groupe de trois fréquences de base.
Mais ce qui est le plus remarquable dans ce contexte, c’est que tous ces spectres, aussi différents qu’ils peuvent être dans la répartition de leurs fréquences internes, seront toujours perçus comme appartenant à la même famille (Pour donner une analogie concrète et assez simple, je prendrai l’exemple d’un accord harmonique classé qui peut se comporter suivant des écarts d’intervalles très grands mais qui conserve toujours sa couleur et sa fonction propre. L’accord de dominante sur sol peut s’écrire : (sol-si-ré-fa), (si-ré-fa-sol), (ré-fa sol-si), (fa-sol-si-ré)… (sol-ré-fa-si), (sol-fa-si-ré), (sol-si-fa-ré)… (si-ré-sol-fa), (si-fa-ré-sol), (si-sol-ré-fa)… les registres sur lesquels chacune de ces notes sera jouée pouvant être différent à chaque fois, nous obtiendrons toujours ce que nous reconnaissons comme une accord de dominante sur sol.). Les trois fréquences de base seront toujours présente dans ces spectres et en constitueront, en quelque sorte, la « matrice harmonique ». Il est évident que, sauf dans le cas où ces fréquences sont accordées à l’unisson, les spectres ainsi obtenus engendrent des configurations hautement inharmoniques, la densité de l’inharmonicité étant consécutive à la complexité des rapports harmoniques qu’entretiennent ces trois fréquences entre elles.
Gilbert Nouno a adapté cet algorithme afin qu’il soit utilisable dans le contexte du quatuor à cordes. Chacune de ces trois fréquences sera donc choisie dans le jeu des instruments, une matrice de connexion indiquant, section par section, lesquels, parmi ces quatre musiciens, auront en charge la création de ces spectres. A chaque détection d’une nouvelle note dans le jeu instrumental, un nouveau spectre se créé. Ce qui ressort de cette partition virtuelle est ce que l’on pourrait appeler une « inharmonisation » de la partie instrumentale. On peut avancer que cette dernière représente un sous-ensemble de ce que produit la partie électronique car il est en effet possible de reconnaître toute la partie instrumentale dans la partie de synthèse. En d’autres termes, tout ce qui est joué par les instruments est présent dans la musique de synthèse, cette dernière augmentant le discours musical par la production de spectres dont les caractéristiques (in)harmoniques dépendent des relations intervalliques qui se créent au moment même où les musiciens jouent la partition.
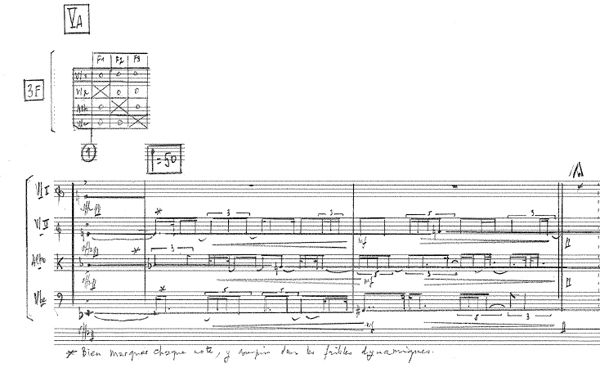
Voici un premier exemple dans lequel trois instruments jouent sur des notes répétées, chacune des attaques, détectée par le programme, provoquant la création d’un nouveau spectre inharmonique. Comme on sait qu’à partir d’une même collection de 3 fréquences, on peut obtenir des complexes de synthèse sonore très variés, il s’en suit une grande variété spectrale appartenant à une même famille inharmonique. Le graphique, indiqué en haut à gauche, indique quels instruments sont connectés avec chacun de ces trois paramètres nécessaires à la production de ce type de synthèse (f1, f2 et f3).
Voici un autre exemple, plus mobile, dans lequel, une musique de pizzicati provoque l’émergence d’une partition 3F, dont les valeurs de durées sont très réduites afin de se trouver en cohérence sonore avec les pizzicati instrumentaux :
Il me faut aborder maintenant un autre principe qui a été mis en œuvre à partir de ce modèle de synthèse : sa réactivité au jeu instrumental. C’est ici qu’intervient un élément qui me semble très important pour établir une connexion « organique » avec le monde instrumental, je veux parler du rôle des descripteurs audio. Il est tout à fait souhaitable que, dans le monde du temps réel, on puisse établir un contrôle de la réactivité avec laquelle un mode de synthèse va intervenir à partir du jeu instrumental. Les descripteurs audio fournissent différents types d’analyse en temps réel des comportements sonores produits par les instruments : leurs hauteur, leurs centres de gravité spectrale, leurs brillances, leurs durées, etc. Dans Tensio, j’ai limité mon choix à l’analyse de la durée des sons instrumentaux qui agit comme un critère sélectif qui décidera si le modèle 3F produira, ou non un spectre nouveau. Le modèle intervient alors que sous certaines conditions et restera muet si ces conditions ne sont pas remplies. Comme on le voit dans la partition ci-dessous, les instruments alternent entre des notes répétées de durées moyennes et des groupes de notes devant être jouées dans une très grande vitesse. En fixant un seuil de durée très bref, j’ai choisi ici que le modèle agisse uniquement dans le cas où les notes jouées excèdent cette durée. Le modèle alors attend que cette durée soit atteinte pour effectuer le calcul nécessaire à la composition des spectres. La musique de synthèse produit alors une couche assez stable et régulière et « ignore » toute les petites figures intermédiaires entre les notes tenues :
L’exemple suivant reproduit la situation précédent mais en négatif : le modèle 3F reste « sourd » aux notes tenues et n’intervient que lors des petites notes très rapides. La musique de synthèse accompagne alors les mouvements vifs et instables des instruments :
Le rôle des descripteurs audio est, à mon sens, promu à un brillant avenir et c’est eux lui que devraient que devrait se concentrer une partie des recherches musicales aujourd’hui. Dans leurs états actuels, ils ne sont pas encore tout à fait adaptés aux besoins compositionnels, si ce n’est dans l’analyse précise de composants de base tels que la hauteur et la durée. Mais il semble qu’il y ait un grand intérêt à développer leur usage dans des domaines plus complexes tels que leurs caractéristiques spectrales.
6) Les échelles dérivées de la structure spectrale.
La synthèse 3F produit des divisions de l’espace des hauteurs tout à fait irrégulières et variables. Irrégulières dans le sens ou les intervalles de séparations entre les différents partiels des spectres peuvent être parfois extrêmes et ne produisent pas des écarts identiques. Variables car chaque nouvelle note jouée par un instrument provoque, si aucun critère sélectif n’est appliqué, un nouveau calcul de spectre dont les raies fréquentielles ne correspondront que dans des cas très rares avec le précédent. Cette grande richesse et cette grande complexité de comportements m’ont incité à chercher à trouver des conséquences musicales qui dépassent la simple construction de spectres inharmoniques. J’ai alors de nouveau utilisé une méthode que j’avais expérimentée, voilà plus de 25 ans, dans Zeitlauf, ma toute première composition électronique composée en 1980. Le principe en était le suivant : il s’agissait de créer des divisions de l’espace sonore des hauteurs (des striages en quelque sortes) dont la construction serait une « homothétie » de la structure interne de spectres inharmoniques. Pour donner un exemple simple, imaginons un spectre harmonique, composé d’une superposition d’intervalles tels que l’octave, la quinte, la quarte, les tierces majeure et mineures, le ton, le demi-ton, etc. On utilise alors cette structure d’intervalle pour créer une échelle sonore sur laquelle se transposera le spectre harmonique. Maintenant, si l’on change la constitution interne du spectre, on modifie du même coup l’échelle et donc l’ensemble des positions sur lesquelles ce spectre va se produire. Ainsi un spectre dont les raies fréquentielles seraient tassées dans une petit ambitus (tel une sorte de petit cluster) évoluera dans un espace très concentré, tandis qu’un spectre composé de grands intervalles évoluera dans un espace au contraire beaucoup plus large. J’ai reproduit ce schéma dans Tensio avec la composition d’échelles sonores dont les pas sont dérivés directement des évolutions successives des spectres calculés avec la méthode 3F. C’est sous la forme d’un continuum de pizzicati, joué par le programme Synful, que ces échelles vont se produire. Ces pizzicati vont se promener sur les différents pas de ces échelles, échelles qui, il faut le rappeler, seront en constante évolution à chaque nouveau calcul d’un spectre. L’ensemble de ces mouvements mélodiques sera organisé suivant un schéma basé sur des chaines de Markov, que Miller Puckette avait mis au point voici plusieurs années. Il s’agit de calculer les probabilités de succession entre différents pas d’un échelle donnée suivant certains paramètres comme les mouvements conjoint ou disjoints, l’ambitus général à l’intérieur duquel les mouvements mélodiques vont se déployer, le tempo, la régularité ou l’irrégularité rythmique, etc. Pour cela il faut tout d’abord définir une échelle abstraite avec des poids successifs indiquant les probabilités d’apparition de chacun de ses pas, puis faire la correspondre avec les fréquences obtenues par les calculs des spectres 3F.
Voici un premier exemple de ce principe. Ici les quatre instruments du quatuor partent d’un unisson, puis par glissandi successifs, aboutissent à un cluster avant de revenir, toujours par glissandi, à l’unisson initial sur la note « mi ». Lors des unissons sur ce mi, il s’ensuit que les 3 fréquences génératrices des spectres seront les mêmes et produiront donc des spectres tout à fait harmoniques ayant comme fréquences fondamentales la note mi. Les échelles dérivées de ces spectres reproduiront alors les fréquences harmoniques (mi à l’octave, si, mi, sol#, si, do#, ré…), qui seront jouées par le continuum des pizzicati. Lors des glissandi et de leurs aboutissements sur ce cluster, ces échelles deviendront de plus en plus complexes car les rapports d’intervalles entre les notes jouées par quatuor provoqueront une grande inharmonicité spectrale, puis, progressivement, nous entendrons ces pizzicati revenir à l’échelle harmonique initiale au fur et à mesure que les instruments se rejoindront sur l’unisson :
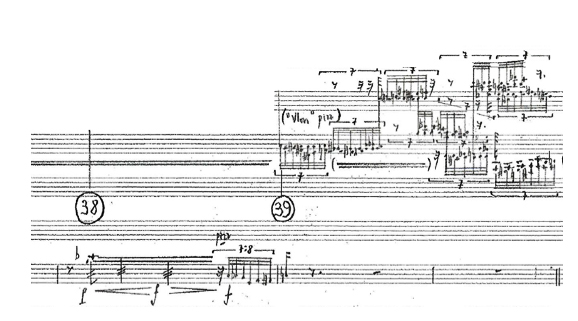
Dans l’exemple suivant, la stabilité des fréquences jouées par le quatuor produit une échelle qui se développe indépendamment après que les musiciens aient cessés de jouer :
Le même procédé se reproduit ici mais, les hauteurs sur lesquelles se stabilisent les instruments étant différentes, il s’en suit des échelles dérivées également différentes :
Pour résumer ce procédé voici les différentes étapes de construction de ces échelles :
a- Les instruments produisent des rencontres de hauteurs qui forment des intervalles
b- Ces hauteurs sont utilisées par groupes de 3, chacune étant extraites de l’analyse fréquentielle dans les trois instruments choisis dans le quatuor (chaque instrument contrôlant soit f1, soit f2, soit f3) et envoyés comme paramètres pour le calcul de spectres sonores.
c- Le moteur de synthèse 3F calcul les spectres sonores suivant les relations d’intervalles entre ces trois fréquences de base
d- Un engendrement d’échelles dérivées est obtenu par homothétie avec la structure interne des raies spectrales des sons produits par la synthèse 3F. Ces échelles évoluent suivant des procédés markoviens et sont produits par des sons pizzicati obtenus par le système de synthèse Synful.
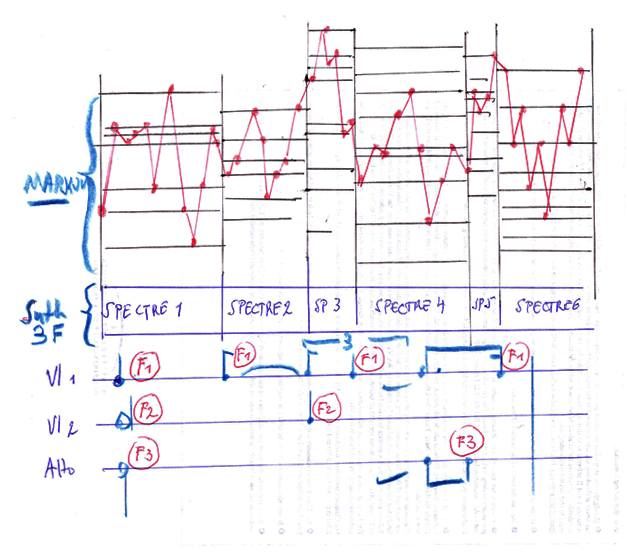
Le graphique suivant aidera à comprendre le processus :
Il y a donc une série de déductions successives entre le jeu instrumental et l’engendrement des échelles sonores, la synthèse 3F se comportant comme le principe intermédiaire entre l’un et l’autre. Dans l’exemple suivant, j’ai éliminé l’étape intermédiaire, non dans son fonctionnement, car la synthèse 3F est un maillon indispensable pour l’engendrement scalaire, mais dans la perception. Le quatuor joue une musique en pizzicati auquel répond les pizzicati de Synful. On entend alors des échelles dérivées de ce que joue le quatuor (et effectivement, les pizzicati joués s’entendent dans les échelles markoviennes produites) mais les sons de synthèse 3F ont disparus. C’est un procédé de composition que j’ai déjà utilisé dans Pluton pour piano et électronique qui consiste à donner à entendre l’action d’un processus sur un autre, mais pas le processus lui-même.
2) Les corrélations harmoniques des toupies sonores.
Les toupies sonores sont un procédé que j’ai utilisé depuis mon opéra K… qui permet de simuler la rotation d’un son sur lui-même. Ce procédé est inspiré du fameux « leslie » » que l’on trouve sur les orgues Hammond sous la forme de deux haut-parleurs coniques actionné par un moteur les faisant tourner circulairement :
C’est Serge Lemouton qui a adapté cet effet dans le programme MaxMsp. Lorsque j’ai utilisé ce système, je l’ai toujours attaché aux harmonizers, ce qui fait que les sons tournent plus ou moins vite où lentement tandis qu’ils sont transposés dans le grave ou dans l’aigu. Je l’ai repris, de façon interactive dans Partita I en donnant le contrôle de ces transpositions et de ces rotations au soliste : lors d’un son en crescendo, on mesure la durée du son ainsi que son énergie finale, et on en déduit l’intervalle de transposition, la durée de son accélération ou de son ralentissement, ainsi que la vitesse qu’il devra atteindre à la fin de cette évolution. J’ai repris ce procédé dans une section de Tensio. Ici on voit les quatre instruments produire des petites poussées d’archet (dont chacune sera analysée en durée et en amplitude) qui provoquent ces brusques transpositions vers l’aigu.
Les durées de ces transpositions ainsi que les évolutions des vitesses respectives des 4 toupies ne sont bien sûr pas connues à l’avance et dépendent uniquement de l’interprétation.
J’ai voulu trouver un procédé plus déterministe pour contrôler ces évolutions des toupies, et j’ai opté pour un système de corrélation entre les transpositions et les vitesses. Il consiste en ceci. Il y a tout d’abord une « toupie-maitresse » qui tourne à une vitesse qui est décidée à l’avance, puis les quatre autres toupies vont s’écarter de cette toupie-maitresses soit, comme précédemment suivant des critères liés à l’analyse des sons instrumentaux, soit de façon plus déterministe. Mais, à chaque mouvement de transposition, l’écart d’intervalle entre la toupie-maitresse et les autres toupies sera mesuré de façon harmonique. Ainsi une toupie sonnant l’une à l’octave de la toupie-maitresse tournera deux fois plus vite, si elle sonne au demi-ton inférieur, elle tournera 1,0594631 fois plus lentement, etc… Le problème, dans ce système, est que les sons vont toujours tourner plus vite au fur et à mesure qu’ils seront transposés vers l’aigu. Pour contrebalancer cette situation j’ai imaginé plusieurs solutions :
a) Un régime absolu lorsque les transpositions seront décorrélées des vitesses. Vitesses et transposition seront contrôlées indépendamment les unes des autres.
b) Un régime relatif lorsque les vitesses seront calculées suivant le rapport harmonique avec la toupie-maîtresse
c) Un régime relatif inversé dans lequel on échange les signes : une transposition vers l’aigu correspondra à une vitesse plus lente, mais tout en respectant la valeur de l’indice harmonique.
d) Un régime modulo qui permet que toutes les toupies qui sonnent à l’octave de la toupie-maitresse tourneront à la même vitesse et seront totalement synchronisées à elle. Dans ce cas, 4 toupies tournant rigoureusement à la même vitesse synchronisées se fondent totalement les unes dans les autres. On n’en entend plus qu’une seule. Les vitesses alors augmentent lorsqu’on progresse vers l’aigu jusqu’à la quarte augmentée (c’est-à-dire la moitié de l’octave) puis ralentissent jusqu’à se synchroniser à la vitesse-maitresse lorsqu’elles atteignent l’octave supérieure.
e) Un régime modulo inversé qui effectue le même parcours mais en ralentissant d’abord jusqu’à la quarte augmentée, puis accélérant à nouveau en allant vers l’octave.
Dans l’exemple suivant les sons électroniques restent assez stables, mais les changements des rotations respectives de chacune d’entre elles dépendent de la modification de ces régimes :
La toute fin de l’œuvre montre une progression lente de toutes les toupies vers l’extrême aigu ce qui les pousse à des vitesses de rotations elles aussi extrêmes, ici 72 fois par secondes. Cette valeur est calculée suivant l’écart d’intervalle qui les sépare de la note la plus grave :
Un autre exemple d’écarts extrêmes de vitesse est donné dans l’extrait suivant dans lequel certaines toupies tournent à moins de 2 rotations par secondes, tandis qu’une autre atteint la vitesse de 141 rotations dans le même temps. Il est évident que de telles vitesses ne sont plus perçues comme des rotations mais se métamorphosent en modulation car de nombreuses nouvelles fréquences se créent par la périodicité de ces rotations :
Enfin, pour terminer sur ce chapitre, voici un « fondu » des 4 toupies en une seule : au fur et à mesure qu’elles s’approchent du « la 440 » qui est la fréquence de la toupie-maîtresse, les 4 toupies se rapprochent de sa vitesse, comme par attraction, et disparaissent à l’intérieur :
3) Sur les temps hétérogènes et leur notation.
La nature des temps musicaux, leur superposition et leur coordination, ont été une des mes sources de préoccupation principale au cours de la composition de cette œuvre. Ces temps obéissent à des lois qui leur sont propres et autonomes, mais cependant doivent se coordonner entre eux, ne serait-ce que d’une manière floue. Les différentes catégories de temps, en musique, sont grandement une affaire de représentation et de notation et ce sont précisément ces modes de représentations diverses qui les définissent. L’absence de notation temporelle a été, pendant très longtemps, un des freins majeurs à la stagnation de la composition avec les outils du temps réel. Ce n’est qu’assez récemment que la situation a pu enfin sortir de ce marasme, contre lequel je n’ai jamais cessé de pester. On doit à Arshia Cont la primauté de ces recherches et la découverte des solutions qui rapprochent, de façon très sensible, le monde instrumental du monde électronique. Son programme Antescofo, surtout connu pour ses capacités de suivi de partitions, offre d’autres avantages que je me suis efforcé de mettre tout de suite en pratique. Avant d’aborder quelques exemples, j’aimerais rappeler qu’avant la création d’Antescofo, il n’y avait pas d’autres solutions pour noter les valeurs temporelles que de les exprimer en millisecondes. Cette solution, si elle l’avantage de l’extrême précision, se révèle tout à fait inadaptée aux besoins de la polyphonie musicale. En effet les mécanismes de synchronisation musicale n’appartiennent pas du tout au monde de l’exactitude mais sont constamment soumis à une logique toute relative et symbolique. L’écriture même des valeurs temporelles (noires, croches, doubles-croches…) en est l’exemple le plus évident. Ces symboles n’expriment que des relations, mais en aucun cas des valeurs absolues. Ils prennent une valeur absolue lors qu’une indication de tempo est donnée et sont, par ailleurs, soumis à de constantes fluctuations. Cette absence de critère commun entre la notation traditionnelle pour les instruments, et celle qu’on utilisait pour la musique électronique a toujours été un obstacle (pas uniquement théorique mais bien perceptuel) à la fusion de ces deux mondes. Ce mur a été désormais franchis et nous allons voir que, non seulement il met en contact deux univers temporels qui ne faisaient que coexister entre eux, mais qu’il permet également superposition de temps hétérogènes, en d’autres termes : la polyphonie.
a) De la notation polyphonique dans la musique électronique.
Examinons la situation. La partition électronique est soumise au suivi de partition et ne se déploie dans le temps que sous certaines conditions, par exemple lorsqu’un événement attendu est joué par un instrument. Dans l’exemple suivant, on voit une ligne de violon déclenchant trois sons successifs en crescendo.
Les instants d’occurrence de ces trois sons ne sont pas connus à l’avance, puisqu’ils dépendent du moment où le violoniste jouera les notes qui doivent les déclencher. Par contre les durées de ces sons sont prédéterminées et scrupuleusement notées dans le programme. Maintenant, ajoutons une autre voix, une succession de pizzicati répétés après un petit retard :
Un système traditionnel de « computer music notation » aurait résolu le problème de la manière suivante :
Evt 1 0.5 « do# »
0.7 « do# »
0.9 « do# »
1.1 « do# »
1.3 « do# »
1.5 « do# »
1.7 « do# »
Si tant est que la valeur de la noire soit égale 60, c’est-à-dire une seconde, on peut facilement arriver à noter un événement comme celui-là. Mais, on l’a vu dans l’exemple suivant, la valeur de la noire correspond à 72. Après un certain nombre de calculs, on peut penser que la chose reste toujours faisable sans trop d’efforts. Maintenant ajoutons encore une voix : une série d’accords et de glissandi superposés :
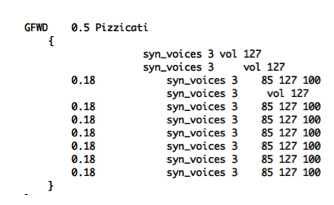
Voila qu’il nous faut calculer maintenant deux temporalités qui se chevauchent : celle des pizzicati et celle des accords. Comment exprimer les débuts de chacun de ces accords dont la métrique ne correspond pas à celle des pizzicati en quintolet ? Ici nous serions en face d’une impossibilité si aucune structure de polyphonie temporelle n’existait dans les systèmes de notations, tel que c’était le cas autrefois. En d’autres termes, lorsque le système ne propose qu’un temps homogène et absolu, il faut pouvoir calculer la différence de temps entre tous les événements appartenant à deux couches, qui elles, ne sont pas toujours exprimées dans une même temporalité. Si tout est humainement possible, voilà ici un cas qui rebuterait toute tentatives de noter une polyphonie avec les moyens de la synthèse. La manière dont Arshia Cont a résolu le problème est la suivante. Il a créé une unité appelée Groupe Forward (GFWD) dont une instance va gérer la voix en pizzicati :
tandis que une autre instance va gérer celle des accords :
Il faut noter que deux formes d’écriture temporelles sont ici utilisées. La section « pizzicati » est exprimée en valeur absolues (chaque note intervenant 0.18’’ après la précédente), tandis que la section « arco tremolo » est notée en valeurs relatives (la formule « @b2 » indiquant que l’événement durera deux temps, la valeur de ces temps (le tempo) étant indiquée ailleurs dans la partition). On peut ainsi ajouter un grand nombre de couches de temps hétérogènes dont chacun aura son propre mode de fonctionnement interne, le programme Antescofo assurera la gestion temporelle de la superposition de toutes ces couches. Comme on le voit, il ne s’agit pas seulement d’une facilité d’écriture qui est fournie ici, mais d’une ouverture à la polyphonie dont l’accès nous était barré par l’indigence des modes de représentation en usage jusqu’alors. Si l’idée que la conception dépend grandement de sa représentation, et donc de l’écriture, devait être encore sujette à caution dans certains esprits, cet exemple permettrait, je l’espère, de faire tomber quelques préjugés.
b) Le suivi de tempo.
La variabilité du tempo est une chose qui est connue depuis longtemps, et les écarts conceptuels (et pas seulement conceptuels) entre une musique mobile et organique dans le traitement de son temps, et une autre figée dans une temporalité rigide a toujours été, pour moi, la principale pierre d’achoppement dans la confrontation de la musique instrumentale et électronique. Les premières œuvres sur bande magnétique étaient le cas le plus extrême de cet écart, mais il faut être juste : le temps réel n’a guère fait avancer les choses dans ce domaine avant une époque récente. Dans bien des cas, les musiques en temps réel n’étaient en fait que des musiques sur bande qui auraient été coupées en petits morceaux aussi rigides les uns que les autres. Le seul point de communication temporel était le début de ces petits morceaux qui pouvaient être soumis à un temps non chronométrique, mais leur devenir n’existait pas. Une autre avancée, toujours liée au programme Antescofo, consiste en un suivi de tempo qui permet de faire s’enchaîner des événements instrumentaux et électroniques dans une parfaite continuité temporelle. J’ai utilisé ce procédé à plusieurs reprises dans Tensio. Voici un premier exemple :
Dans la séquence qui suit, le violon joue un accord tremolo (sans tempo) puis une petite figure en pizzicati en septolets. A cette figure doit répondre un groupe de septolets dans la partie électronique qui doit se trouver en parfaite continuité de tempo avec ce que vient de jouer le violon. C’est par l’intermédiaire du suivi de partitions que va se passer cet échange rythmique. Les pizzicati joués par le violon vont être analysés et sachant qu’il s’agit de septolets de triples croches, la valeur de la noire va être déterminée, et par là même, celle du tempo. Il faut donc ensuite appliquer cette valeur de tempo aux pizzicati joués par la musique électronique :
L’exemple suivant montre un échange de questions/réponses entre le quatuor et l’électronique (qui produit aussi des sons pizzicati) dont le tempo est constamment adapté, c’est-à-dire que la valeur des croches des triolets et analysée pendant toute la séquence et module en quelque sorte la vitesse des notes jouées par les « pizzicati électroniques » :
Ces tempi peuvent être soumis à une grande variabilité et c’est ce que nous allons voir dans le chapitre suivant, consacré à la superposition de temps hétérogènes dans la composition.
c) Les temps hétérogènes.
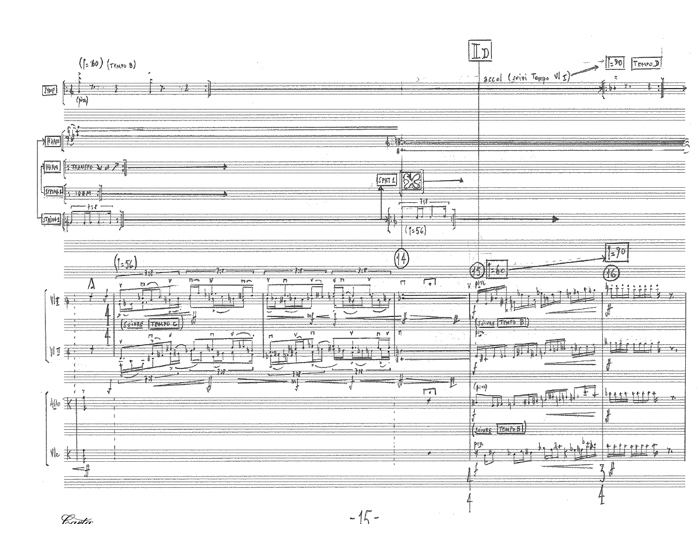
Dans la deuxième section de l’œuvre, j’ai mis au point des structures temporelles qui réagissent les unes aux autres dans un temps fluide et souple. Parfois les instruments donnent le tempo à l’électronique, parfois c’est l’inverse qui se produit, parfois deux tempi sont utilisés, parfois il se produit des événements sans tempo d’aucune sorte. Un coup d’œil sur la partition suivante nous montre la situation. L’événement 9, joué au violon 1 indique un ralenti dont la valeur d’arrivée est envoyée à une voix de synthèse notée comme le « TEMPO B » : il s’agit de la répétition d’une simple note qui aura valeur de métronome pour les instruments. Le « TEMPO A » lui est donné par une autre voix de synthèse jouant une note répétée dans un rythme irrégulier de quintolet. Ces deux tempi sont totalement indépendants les uns des autres et l’alto et le violoncelle joueront une séquence en suivant le métronome (tempo A) tandis que le second violon suivra le tempo B. Ces deux groupes sont libres de commencer quand ils le veulent :
Un peu plus loin dans la partition, nous voyons une première évolution. Les deux violons jouent une succession de doubles croches en septolets dont la valeur de tempo est envoyée à la voix électronique en notes répétées (tempo C) qui va alors modifier le tempo qu’elle avait précédemment (tempo A). Le quintolet est remplacé par un septolet dont la valeur de tempo est prise dans la partie du premier violon. Le second groupe (alto et violoncelle) joue alors une deuxième séquence, mais toujours en se référant au tempo du métronome (B) qui, lui, n’a pas changé :
Vient ensuite une autre séquence. Les deux violons suivent le tempo C (celui du septolet installé précédemment) puis, à l’événement 15, tout le quatuor joue une progression en pizzicati qui va subir un accelerando. La valeur finale de cette accélération deviendra la nouvelle valeur du « métronome » (tempo D).
Dans la séquence qui suit, nous voyons à nouveau le groupe alto/violoncelle se synchroniser sur le tempo C (en septolets) tandis que les deux violons jouent une nouvelle séquence sur le nouveau tempo D :
Nous voyons ensuite un autre cas de figure à l’événement 17. Un nouveau tempo (Tempo E) est fixé arbitrairement dans la partie électronique dans une figure articulée par 9:8, qui sert d’étalon pour la séquence jouée cette fois par les quatre instruments :
Enfin, dans ce dernier exemple, on voit à l’événement 20 un nouvel accelerando qui va modifier une nouvelle fois le « métronome » sur lequel tous le quatuor va se synchroniser pour jouer cette séquence en triolets dans un tempo très vif :